Masse Feder System, Reglersynthese durch LQR

In diesem Notebook wollen wir die Reglersynthese mittels LQR (Linear Quadratischer Regler) durchführen. Seine Synthese ist der Teil der optimalen Regelung. Als erstes wollen wir kurz die dynamische Programmierung wiederholen. Die dynamische Programmierung ist sowohl für die optimale Regelung als auch für das bestärkende Lernen zentral.

import numpy as np
import scipy
import scipy.signal as signal
import matplotlib.pyplot as plt

m1 = 1
d1 = 0.15
c1 = 0.3

m2 = 1
d2 = 0.15
c2 = 0.3

d3 = 0.15
c3 = 0.3

A = np.array([[0., 0., 1., 0.],
              [0., 0., 0., 1.], 
              [-(c1+c2)/m1, c2/m1, -(d1+d2)/m1, d2/m1],
              [c2/m2, -(c2+c3)/m2, (d2)/m2, -(d2+d3)/m2]])
B = np.array([[0., 0.], [0., 0.], [1./m1, 0.], [0., 1/m2]])
C = np.array([[1., 0., 0., 0], [0., 1., 0., 0.]])
D = np.array([[0., 0.],[0., 0.]])

sys_c = signal.StateSpace(A, B, C, D)

dt = 0.1
sys_d = sys_c.to_discrete(dt)

R = np.eye(2)*1
Q = np.eye(4)*1

Endlicher Zeithorizont

Dynamische Programmierung für nichtlineare Systeme

Betrachten wir das zeitdiskrete System

$x_{k + 1} = f_{k} (x_{k}, u_{k})$

auf ein Intervall $k \in [i, N]$ , mit dem Anfangswert $x_{i}$ . Nun soll das Gütefunktional

$J_{i} (x_{i}) = ϕ (x_{N}, N) + \sum_{i = 1}^{N - 1} c_{k} (x_{k}, u_{k})$

minimiert werden. Angenommen wir haben schon eine optimale Regelung von einem gegeben Zustand $x_{k + 1}$ zum Zeitpunkt $k + 1$ . Die optimalen Eingänge sind mit $u_{k + 1}, u_{k + 2}, \dots, u_{N - 1}$ gegeben, die auf die optimale Kosten $J_{k + 1}^{*} (x_{k + 1})$ führen. Wenn wir einen beliebigen (nicht notwendigerweise optimalen) Eingang $u_{k}$ zum Zustand $x_{k}$ und Zeitpunkt $k$ aufschalten, dann ergeben sich die akkumulierten Kosten

$J_{k} (x_{k}, u_{k}) = c_{k} (x_{k}, u_{k}) + J_{k + 1}^{*} (x_{k + 1}) .$

Nach Bellman, können die optimalen Kosten zum Zeitpunkt mit

$J_{k}^{*} (x_{k}) = \underset{u_{k}}{m i n} (c_{k} (x_{k}, u_{k}) + J_{k + 1}^{*} (x_{k + 1}))$

angegeben werden. Wenn als schon eine Teillösung bekannt ist, müssen wir nur eine Optimierung zum Zeitpunkt $k$ durchführen. Die Rekursion läuft vom Zeitpunkt $k + 1 = N$ rückwärts bis zum Startzeitpunk $k = 0$ . Es sei darauf hingewiesen, dass es notwendig ist über die Summe der beiden Terme $(c_{k} (x_{k}, u_{k}) + J_{k + 1}^{*} (x_{k}))$ zu minimieren, weil auch $x_{k + 1}$ mit $x_{k + 1} = f_{k} (x_{k}, u_{k})$ eine Funktion von $u_{k}$ ist. Eine alternative Formulierung macht den Sachverhalt mit

$J_{k}^{*} (x_{k}) = \underset{u_{k}}{m i n} (c_{k} (x_{k}, u_{k}) + J_{k + 1}^{*} (f_{k} (x_{k}, u_{k})))$

besser ersichtlich.

Dynamische Programmierung für lineare Systeme

Gegeben sei ein lineares zeitdiskretes System

$x_{k + 1} = A x_{k} + B u_{k}$

mit dem Gütefunktional

$J_{0} (x_{0}) = \frac{1}{2} x_{N}^{T} S_{N} x_{N} + \frac{1}{2} \sum_{k = 0}^{N - 1} (x_{k}^{T} Q x_{k} + u_{k}^{T} R u_{k})$

mit $ S_N , Q , R > 0 $. Wir wenden nun das Prinzip der Optimalität an und starten mit

$J_{N}^{*} (x_{N}) = \frac{1}{2} x_{N} S_{N} x_{N}$

zum Zeitpunkt $N$ und gehen rückwärts zu $N - 1$ und erhalten

$\begin{aligned} J_{N - 1} (x_{N - 1}) & = \frac{1}{2} (x_{N - 1}^{T} Q x_{N - 1} + u_{N - 1}^{T} R u_{N - 1}) \\ + \frac{1}{2} (A x_{N - 1} + B u_{N - 1})^{T} S_{N} (A x_{N - 1} + B u_{N - 1}) \end{aligned}$

durch einsetzen der Dynamik. Weil wir keine Beschränkungen auf Aktionen $u$ berücksichtigen müssen, kann das Minimum $J_{N - 1}$ einfach aus dem Gleichsetzen des Gradienten mit Null

$\begin{array}{r} 0 = \nabla_{u_{N - 1} J_{N - 1}} = R u_{N - 1} + B^{T} S_{N} (A x_{N - 1} + B u_{N - 1}) \\ u_{N - 1}^{*} = - \underset{K_{N - 1}}{\underset{⏟}{(B^{T} S_{N} B + R)^{- 1} B^{T} S_{N} A}} x_{N - 1} \end{array}$

errechnet werden. Wenn nun die optimale Aktion $u_{N - 1}^{*} = - K_{N - 1} x_{N - 1}$ in die Fortsetzungskosten eingesetzt wird erhält man die optimalen Fortsetzungskosten

$J_{N - 1}^{*} = \frac{1}{2} x_{N - 1}^{T} \underset{S_{N - 1}}{\underset{⏟}{[(A - B K_{N - 1})^{T} S_{N} (A - B K_{N - 1}) + K_{N - 1}^{T} R K_{N - 1} + Q]}} x_{N - 1} .$

Ein wiederholtes Vorgehen von $k = N - 2, N - 3, \dots$ löst das Optimierungsproblem.

Code

Hinweis

Rückwärts Rekursion

$\begin{aligned} for k = N - 1 to 0 : \\ (finale Kosten P_{N} = S_{N}) \\ P_{k} = Q + A^{T} P_{k + 1} A - A^{T} P_{k + 1} B (R + B^{T} P_{k + 1} B)^{- 1} B^{T} P_{k + 1} A \\ K_{k} = (R + B^{T} P_{k + 1} B)^{- 1} B^{T} P_{k + 1} \end{aligned}$

Vorwärts Rekursion

$\begin{aligned} for t = 0 to N - 1 : \\ u_{k} = - K_{k} x_{k} \\ x_{k + 1} = A x_{k} + B u_{k} \end{aligned}$

def LQR_DP(A,B,Q,R,N):
    """ executes the dynamic program for the discrete time finite horizon LQR (N-steps)
        returns: final controller, final value-function, controller (every-step), value-function (every-step)
    """
    P = np.zeros(sys_d.A.shape)
    P_array = np.zeros((N,P.shape[0],P.shape[1]))
    K_array = np.zeros((N,B.shape[1],B.shape[0]))
    for k in range(N-1,-1,-1):
        #print(k)
        P = Q+A.T@P@A-A.T@P@B@np.linalg.inv(R+B.T@P@B)@B.T@P@A
        P_array[k,:,:] = P
        K = np.linalg.inv(R+B.T@P@B)@B.T@P@A
        K_array[k,:,:] = K
    return K, P, K_array, P_array

N = 100
K, P, K_array, P_array = LQR_DP(sys_d.A,sys_d.B,Q,R,N)
K

array([[0.525914  , 0.14589593, 1.15336293, 0.20646155],
       [0.14589593, 0.525914  , 0.20646155, 1.15336293]])

Unendlicher Zeithorizont

In diesem Abschnitt werden wir das Problem

$J (x_{0}) = \frac{1}{2} \sum_{k = 0}^{\infty} (x_{k}^{T} Q x_{k} + u_{k}^{T} R u_{k})$

unendlichem Zeithorizont besprechen.

Riccati Gleichung Herleitung (Schematisch)

Für die Herleitung der Riccati Gleichung versuchen wir den Ansatz

$J^{*} (x_{k}) = \sum_{i = k}^{\infty} x_{i}^{T} (Q + K_{*}^{T} R K_{*}) x_{i} = x_{k}^{T} P_{*} x_{k}$

für die Cost-to-Go Funktion.

Die optimale Bellmangleichung mit obigem Ansatz lautet

$\begin{aligned} J^{*} (x_{k}) & = min_{u_{k}} c (x_{k}, u_{k}) + J^{*} (x_{k + 1}) \\ = min_{u_{k}} c (x_{k}, u_{k}) + J^{*} (A * x_{k} + B * x_{k}) \\ = min_{u_{k}} (x_{k}^{T} Q x_{k} + u_{k}^{T} R u_{k} + (A x_{k} + B u_{k})^{T} P_{*} (A x_{k} + B u_{k})) \end{aligned}$

Durch das Nullsetzen und das Ableiten nach $u_{k}$

$\frac{\partial}{\partial u_{k}} (x_{k}^{T} Q x_{k} + u_{k}^{T} R u_{k} + (A x_{k} + B u_{k})^{T} P_{*} (A x_{k} + B u_{k})) = 0$

erhalten wir

$R u_{k} + B^{T} P_{*} (A x_{k} + B u_{k}) = 0$

womit sich das Regelgesetz

$u_{k} = - \underset{K_{*}}{\underset{⏟}{(R + B^{T} P_{*} B)^{- 1} B^{T} P_{*} A}} x_{k}$

ergibt. Die Regelparameter können also mit

$K_{*} = (R + B^{T} P_{*} B)^{- 1} B^{T} P_{*} A$

berechnet werden sobald die optimale $P_{*}$ Matrix bekannt ist. Eliminieren wir $u_{k}$ durch das Einsetzen in die obige Gleichung

$x_{k}^{T} P_{*} x_{k} = x_{k}^{T} Q x_{k} + u_{k}^{T} R u_{k} + (A x_{k} + B u_{k})^{T} P_{*} (A x_{k} + B u_{k})$

erhalten wir die zeitdiskrete algebraische Riccati-Gleichung (DARE)

$A^{T} P_{*} A - P_{*} + Q - A^{T} P_{*} B (R + B^{T} P_{*} B)^{- 1} B^{T} P_{*} A = 0.$

Diese Gleichung ist wohl eine der berühmtesten Gleichungen der Regelungstheorie. Es stehen effizient Methoden zum Lösen dieser Gleichung zur Verfügung.

Code

Hinweis

1. Riccati Gleichung

$0 = A^{T} P A - P + Q - A^{T} P B (R + B^{T} P B)^{- 1} B^{T} P A$

2. Regler Synthese

$K = (R + B^{T} P B)^{- 1} B^{T} P A$

def dlqr(A,B,Q,R):
    """ solves the discrete time infinite horizon LQR problem
        returns: controller, matrix of the value function, closed loop eigenvalues
    """
    
    #first, try to solve the ricatti equation
    P = np.matrix(scipy.linalg.solve_discrete_are(A, B, Q, R))
 
    #compute the LQR gain
    K = np.matrix(scipy.linalg.inv(B.T@P@B+R)@(B.T@P@A))
 
    eigVals, eigVecs = scipy.linalg.eig(A-B@K)
 
    return K, P, eigVals

K_infinite, P_infinite, eigVals_closed = dlqr(sys_d.A,sys_d.B,Q,R)
print(P_infinite)
print(K_infinite)

[[16.26397985  0.33991886  5.9558398   1.49377766]
 [ 0.33991886 16.26397985  1.49377766  5.9558398 ]
 [ 5.9558398   1.49377766 12.68398729  2.19092355]
 [ 1.49377766  5.9558398   2.19092355 12.68398729]]
[[0.52591444 0.14589589 1.15336362 0.20646134]
 [0.14589589 0.52591444 0.20646134 1.15336362]]

Vergleich

P_infinite_plot = np.broadcast_to(P_infinite, (N, *P_infinite.shape)).reshape(N,4*4)
K_infinite_plot = np.broadcast_to(K_infinite, (N, *K_infinite.shape)).reshape(N,2*4)

P_array_plot = P_array.reshape(N,4*4)
K_array_plot = K_array.reshape(N,2*4)

plt.plot(P_infinite_plot, color='black', linestyle='--');
plt.plot([], [], 'black', linestyle='--' , label='infinite') # helper plots for legend
plt.plot(P_array_plot, color='black');
plt.plot([], [], 'black', label='finite') # helper plots for legend
plt.legend()
plt.grid()
plt.ylabel('Elements of P')
plt.xlabel('time')

Text(0.5, 0, 'time')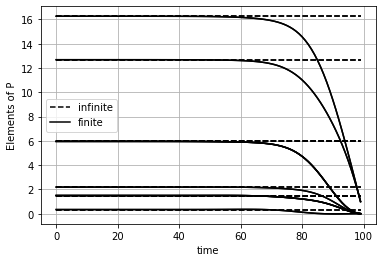

plt.plot(K_infinite_plot, color='black', linestyle='--');
plt.plot([], [], 'black', linestyle='--' , label='infinite') # helper plots for legend
plt.plot(K_array_plot, color='black');
plt.plot([], [], 'black', label='finite') # helper plots for legend
plt.legend()
plt.grid()
plt.ylabel('Elements of K')
plt.xlabel('time')

Text(0.5, 0, 'time')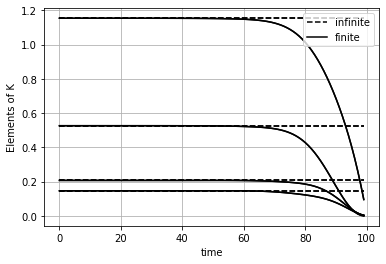

Das Problem mit endlichen Zeithorizont führt auf einen Regler $K_{k}$ welcher von der Zeit abhängig ist. Das Problem mit unendlichen Zeithorizont führt hingegen auf eine konstantes Regelgesetz $K$ .

Die Regelparameter unterscheiden sich erst gegen Ende des Zeithorizonts deutlich.

Fazit

Wir haben hier die dynamische Programmierung besprochen. Für Probleme mit unendlichen Zeithorizont ist das Lösen der Riccati Gleichung die effizienteste Methode sobald ein gutes Modell vorhanden ist. Jedoch gibt es viele weitere Möglichkeiten das LQR Problem zu lösen.

Im den nächsten Blogeinträgen wollen wir Methoden aus der Künstlichen Intelligenz Forschung besprechen. Dazu führen wir aber eine etwas andere Notation ein.