import numpy as np
import control as ct
import matplotlib.pyplot as plt
from matplotlib import patches
plt.style.use('ggplot')Das Frequenzkennlinienverfahren (FKL) ist ein bewährtes und einfaches Entwurfsverfahren und gehört zu den klassischen Verfahren der Regelungstechnik. Dieses Verfahren erlaubt einen Entwurf eines Reglers, welcher gut an die konkrete Strecke angepasst ist.
Vereinfachtes Schnittpunktkriterium
Das vereinfachte Schnittpunktkriterium erlaubt einen Reglerentwurf, wo nur die Phasenreserve berücksichtigt werden muss, aber die Stabilität garantiert wird. Dadurch ist der Entwurf besonders leicht durchzuführen.
Der einfache Typ
Der einfache Typ
Eine realisierbare Übertragungsfunktion \(L(s)\),
\[ L(s) = V \frac{z(s)}{s^{\rho}n(s)} \qquad \rho \in \{0,1\} \]
mit teilerfremden Polynomen \(z(s), s^{\rho}, z(0)=n(0)=1\) und Hurwitz-Polynom \(n(s)\) heißt vom einfachen Typ, wenn sie folgende Bedingungen erfüllt.
- (1a) Die Betragskennlinie von \(L(j\omega)\) weist genau einen Schnittpunkt mit der \(0\)-dB Linie auf, und verläuft für \(\omega \rightarrow \infty\) unter dieser.
- (1b) Die Ortskurve von \(L(jw)\) schneidet für \(0 \leq \omega < \infty\) den Einheitskreis in der \(L\)-Ebene genau einmal, und verbleibt für \(\omega \rightarrow \infty\) im Inneren des Einheitskreises.
- Der Verstärkungsfaktor \(V\) ist positiv, d.h. es gilt \(V > 0\).
Durchtrittsfrequenz
Die Durchtrittsfrequenz \(\omega_c\) ist diejenige Kreisfrequenz, bei der die Ortskurve \(L(j\omega)\) des offenen Kreises den Einheitskreis schneidet, bzw. bei der die Betragskennlinie \(\left|L(j\omega)\right|_{\text{db}}\) die \(0\)-dB Linie schneidet, d.h.
\[ \left| L(j\omega_c) \right| = 1 \qquad \text{bzw.} \qquad \left| L(j\omega_c) \right|_{dB} = 0 \]
Phasen- und Amplitudenreserve
Die Phasenreserve \(\phi_m\) ist der Abstand der Phasenkennlinie von \(L(j\omega)\) an der Stelle \(\omega = \omega_c\) zu \((-180^{\circ})\), d.h.
\[ \phi_m = \arg L(k\omega_c) + 180^{\circ}. \]
Bezeichnet man mit \(\omega_{g}\) diejenige Frequenz, bei der \(L(j\omega_g) = - 180^°\) gilt, so ergibt sich für die sogenannten Amplitudenreserve
\[ g_m = \frac{1}{L(j\omega_g)} \]
Das control Modul liefert einige Methoden um die Phasenreserve und den Amplitudenreserve zu berechnen.
s = ct.tf('s')
G = 0.5/(s*(1+s)*(1+2*s))
#G = (s-1)/(s**2+s+4)
gm, pm, wg, wp = ct.margin(G)
print(f"{gm = :.2f} {pm = :.2f} {wg = :.2f} {wp = :.2f}")
gm, pm, sm, wg, wp, ws = ct.stability_margins(G)
print(f"{gm = :.2f} {pm = :.2f} {wg = :.2f} {wp = :.2f}")gm = 3.00 pm = 32.61 wg = 0.71 wp = 0.37
gm = 3.00 pm = 32.61 wg = 0.71 wp = 0.37Die Methode control.bode erlaubt das automatisierte Einzeichnen der Phasen - und Amplitudenreserve.
plt.figure(figsize=(16,8))
_ = ct.bode(G, margins=True)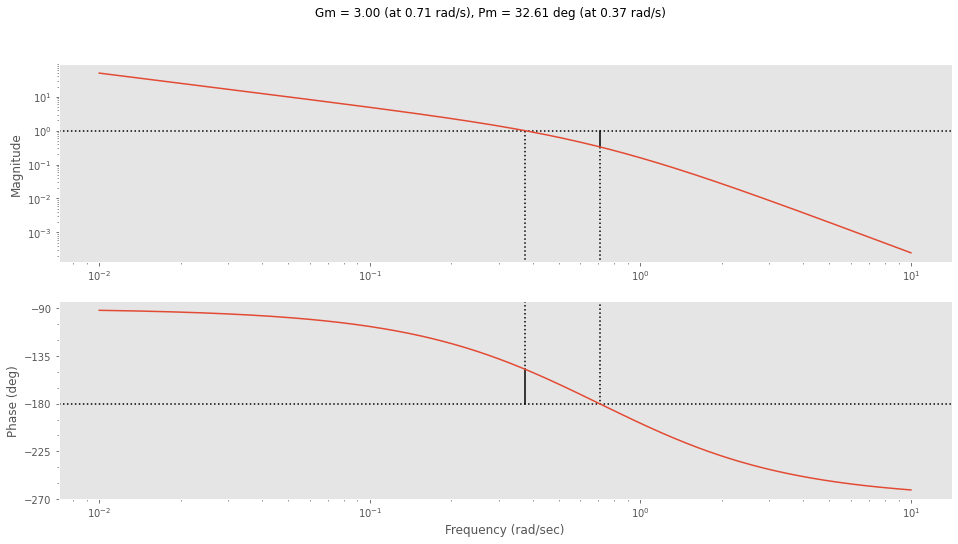
Die Methode control.nyquist zeichnet das Nyquist-Diagramm. Das Einzeichnen der Phasen- und Amplitudenreserve muss hier jedoch “per Hand” erfolgen.
# create pointer
pointer_pm = np.exp(1j*(np.pi+pm*np.pi/180))
# nyquist plot
plt.figure(figsize=(16,8))
_ = ct.nyquist(G)
circle_uc = plt.Circle((0, 0), 1, color='black', fill=False)
plt.gca().add_patch(circle_uc)
plt.gca().set_aspect('equal', 'box')
# gain margin
plt.plot([0,-1/gm ],[0.2,0.2],color='blue')
plt.annotate(r'$-1/G_M$',
xy=(-1/gm-0.2, 0.4), xycoords='data',
xytext=(1, 1), textcoords='offset points', size=10)
# phase margin
arc_phi = patches.Arc((0, 0), 2, 2, linewidth=2, color='blue', angle=180.0, theta1=0.0, theta2=pm)
plt.gca().add_patch(arc_phi)
plt.plot([0,np.real(pointer_pm)],[0,np.imag(pointer_pm)],color='black')
plt.annotate(r'$\phi$',
xy=(-1.3, -0.4), xycoords='data',
xytext=(1, 1), textcoords='offset points', size=10)
plt.title('Nyquist-Diagramm')
plt.show()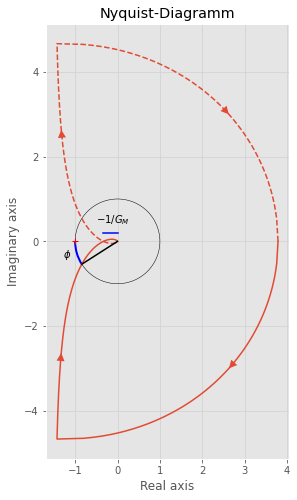
Formulierung des vereinfachten Schnittpunktkriteriums
Durch die oben eingeführten Konzepte, kann das vereinfachte Schnittpunktkriterium folgendermaßen formuliert werden:
vereinfachtes Schnittpunktkriterium
Ist der offene Kreis \(L(s)\) vom einfachen Typ, so ist der geschlossene Regelkreis genau dann BIBO- (und intern) stabil, wenn die Phasenreserve positive ist.
Typisches Entwurfsverfahren
Faustformeln für den Reglerentwurf
Für die Phasenreserve und das Überschwingen gilt der Zusammenhang
\[ \phi_m^{\circ} + ü \approx 70^{\circ}. \]
Es kann durch die Vorgabe des Überschwingens kann auf die Phasenreserve \(\phi_m\) geschlossen werden. Eine kleinere Phasenreserve führt zu einer größeren Schwingneigung des Regelkreises.
Es gilt der Zusammenhang
\[ \omega_c t_r \approx 1.5 \]
zwischen der kritischen Kreisfrequenz \(\omega_c\) und der Anstiegszeit \(t_r\) kann. Dadurch kann durch die Vorgabe der Anstiegszeit die kritische Kreisfrequenz berechnet werde. Eine kleinere Anstiegszeit erfordert eine größere Bandbreite.
Die bleibende Regelabweichung \(e_{\infty}\) für die Testsignale \(r(t) = \sigma(t)\) und \(r(t) = t\) jeweils für \(\rho \in \{0, 1 \}\) sind nachfolgender Tabelle
\[ \begin{split} r(t) &= \sigma(t) \quad \text{bzw.} \quad R(s) = \dfrac{1}{s}: \begin{cases} \rho = 0 \rightarrow e_{\infty} = \dfrac{1}{1+V} \\ \rho = 1 \rightarrow e_{\infty} = 0 \end{cases} \\ r(t) &= t \quad \text{bzw.} \quad R(s) = \dfrac{1}{s^2}: \begin{cases} \rho = 0 \rightarrow e_{\infty} = \infty \\ \rho = 1 \rightarrow e_{\infty} = \dfrac{1}{V} \end{cases} \\ \end{split} \]
zu entnehmen.
Durchführung des Reglerentwurfs
Entwurfsdurchführung
I Umrechnung der gegebenen Regelkreisspezifikation auf den offenenKreis
Im ersten Schritt werden die zeitlichen Vorgaben des geschlossenen Regelkreises, in Frequenz-Vorgaben des offenen Regelkreises umgerechnet. Durch die Anforderung an die Regelabweichung ergeben sich die Vorgaben für \(\rho\) und \(V\).
II Entsprechende Modifikation der Frequenzkennlinien des offenen Kreises
Als erstens werden alle bekannte Teile des offenen Kreises zusammengefügt. Dann können wir diesen offenen Kreis im Bodediagramm analysieren und die Phasenreserve berechnen. Nun müssen Korrekturglieder geschickt eingefügt werden, um die Vorgaben zu erfüllen.
III Simulation des Regelkreises
Eine Simulation des geschlossenen Kreises muss durchgeführt werden, um die Erfüllung der Spezifikation zu überprüfen. Auch das Überprüfen der Stellgröße kann nötig sein.
Fazit
Das hier vorgestellte Verfahren kann auf allgemeinere Strecken wie
\[ L(s) = V \frac{z(s)}{s^{\rho}n(s)}e^{-sL} \qquad \rho \in \{0,1,...\} \]
angewendet werden, wobei dann im Allgemeinen die Stabilitätsprüfung mit dem Nyquistkriterium durchgeführt werden muss. Für Spezialfälle können modifizierte Nyquistkriterien formuliert werden, was die Stabilitätsprüfung wieder vereinfacht. Die Überprüfung der Einhaltung der Spezifikation erfolgt immer mittels einer Simulation, hier mittels der Sprung- oder Rampenantwort.
Referenzen
- Feedback Systems: An Introduction for Scientists and Engineers, Second Edition, 2020/2022 (Karl J. Aström, Richard M. Murray)
- Automatisierungstechnik 2, WS 2019/2020 (Kurt Schlacher)
- Automatisierung, 2021/2022 ACIN (Andreas Kugi)