import control as ctrl
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('ggplot')In diesem Notebook wollen wir aufzeigen was die Regelungstechnik, die Systemidentifikation und das maschinelle Lernen so anspruchsvoll machen kann. Selbst einfache lineare System haben ein reichhaltiges Verhalten.
Die nachfolgenden Überlegungen sind aus dem Buch Adaptive Control, Second Edition [Kark Astrom, Björn Wittenmark] entnommen. Dieses Buch ist gilt als die Standardeinführung in das Gebiet der Adaptiven Regelung. Jedoch werden auch andere Themen wie Systemidentifikation und Verbindungen zum bestärkenden Lernen besprochen. Es sei aber darauf hingewiesen, dass die Inhalte des Buchs den Stand von 1995, (2008) widerspiegeln. Alle Felder, aber insbesondere das Feld des Bestärkenden Lernens haben sich seitdem enorm entwickelt.
Verschiedene Systemantworten offene Systeme
Als erstes wollen wir ein System untersuchen dessen Systemantwort im offenen Regelkreis sehr sensitive auf Parameterschwankungen reagiert.
Offene Systemantworten
Betrachten wir die offene Übertragungsfunktion
\[ G = \frac{1}{(s+1)(s+\color{red}a)} \]
mit dem Parameter \(\color{red}a\) welcher die Werte \(-0.01, 0, 0.01\) annehmen kann.
s = ctrl.tf('s')
a=-0.01
G1 = 1/((s+1)*(s+a))
a= 0
G2 = 1/((s+1)*(s+a))
a= 0.01
G3 = 1/((s+1)*(s+a))t = np.arange(0,300,0.01)_, yout1 = ctrl.step_response(G1,t)
_, yout2 = ctrl.step_response(G2,t)
_, yout3 = ctrl.step_response(G3,t)plt.plot(t,yout1,label="$a=-0.01$")
plt.plot(t,yout2,label="$a= 0$")
plt.plot(t,yout3,label="$a= 0.01$")
plt.legend()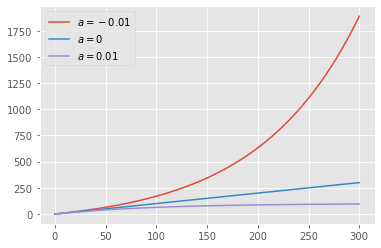
ctrl.bode(G1,label="$a=-0.01$")
ctrl.bode(G2,label="$a= 0$")
ctrl.bode(G3,label="$a= 0.01$")
plt.legend()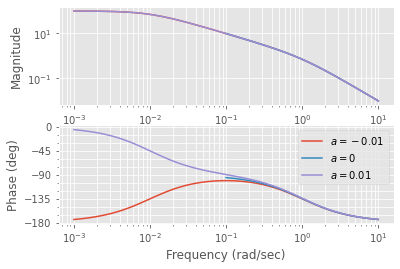
Die Dynamik dieser Übertragungsfunktion sind sehr verschieden. Aus der Systemtheorie wissen wir das System mit \(a=0.01\) stabil ist, die anderen sind instabil. Der erste Teil der Sprungantwort verhält sich für jedes System ähnlich.
Die Bodediagramme unterscheiden sich erheblich bei niedrigen Frequenzen, während diese bei hohen Frequenzen praktisch ident sind.
Geschlossene Systemantworten
Nun wollen wir die Sprungantwort des geschlossenen System untersuchen. Dafür werden alle 3 Systeme mit -1 rückgekoppelt.
L1 = ctrl.feedback(G1,1)
L2 = ctrl.feedback(G2,1)
L3 = ctrl.feedback(G3,1)t = np.arange(0,20,0.01)_, yout1 = ctrl.step_response(L1,t)
_, yout2 = ctrl.step_response(L2,t)
_, yout3 = ctrl.step_response(L3,t)plt.plot(t,yout1,label="$a=-0.01$")
plt.plot(t,yout2,label="$a= 0$")
plt.plot(t,yout3,label="$a= 0.01$")
plt.legend()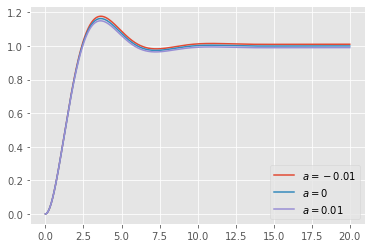
ctrl.bode(L1,label="$a=-0.01$")
ctrl.bode(L2,label="$a= 0$")
ctrl.bode(L3,label="$a= 0.01$")
plt.legend()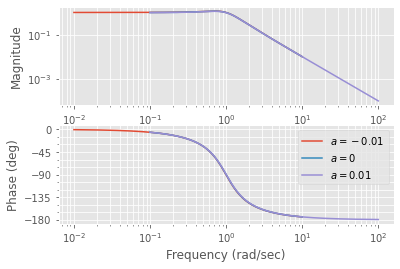
Betrachten wir diese Sprungantworten sehen wir das sich die geschlossenen Systeme sehr ähnlich verhalten. Zusammengefasst, Systeme welche sich im offenen Regelkreis sehr verschieden reagieren, können im geschlossenen Regelkreis ein sehr ähnliches Verhalten zeigen.
Das ist jedoch nicht immer so. Im nächsten Abschnitt untersuchen wir den umgekehrten Fall.
Ähnliche Systemantworten offene Systeme
Betrachten wir die offene Übertragungsfunktion
\[ G = \frac{400(1-s\color{red}T)}{(s+1)(s+20)(1+\color{red}Ts)} \]
mit dem Parameter \(\color{red}T\) welcher die Werte \(0.03, 0, 0.015\) annehmen kann.
Offene Systemantworten
s = ctrl.tf('s')
T= 0.03
G1 = 400*(1-s*T)/((s+1)*(s+20)*(1+T*s))
T= 0
G2 = 400*(1-s*T)/((s+1)*(s+20)*(1+T*s))
T= 0.015
G3 = 400*(1-s*T)/((s+1)*(s+20)*(1+T*s))t = np.arange(0,5,0.01)_, yout1 = ctrl.step_response(G1,t)
_, yout2 = ctrl.step_response(G2,t)
_, yout3 = ctrl.step_response(G3,t)plt.plot(t,yout1,label="$T= 0.03$")
plt.plot(t,yout2,label="$T= 0$")
plt.plot(t,yout3,label="$T= 0.015$")
plt.legend()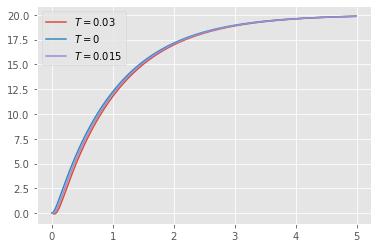
ctrl.bode(G1,label="$T= 0.03$")
ctrl.bode(G2,label="$T= 0$")
ctrl.bode(G3,label="$T= 0.015$")
plt.legend()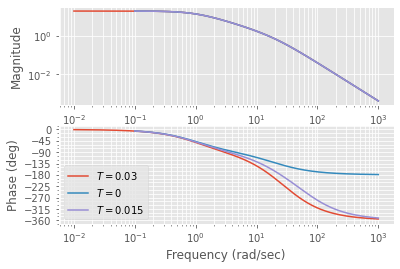
Die Sprungantworten der offenen Systeme erscheinen sehr ähnlich.
Die Bode-Diagramme unterscheiden sich kaum bei niedrigen Frequenzen, während diese bei hohen Frequenzen sehr verschieden sind.
Geschlossene Systemantworten
t = np.arange(0,1,0.01)L1 = ctrl.feedback(G1,1)
L2 = ctrl.feedback(G2,1)
L3 = ctrl.feedback(G3,1)_, yout1 = ctrl.step_response(L1,t)
_, yout2 = ctrl.step_response(L2,t)
_, yout3 = ctrl.step_response(L3,t)plt.plot(t,yout1,label="$T= 0.03$")
plt.plot(t,yout2,label="$T= 0$")
plt.plot(t,yout3,label="$T= 0.015$")
plt.legend()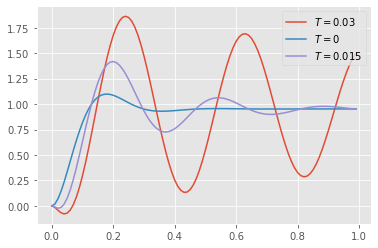
ctrl.bode(L1,label="$T= 0.03$")
ctrl.bode(L2,label="$T= 0$")
ctrl.bode(L3,label="$T= 0.015$")
plt.legend()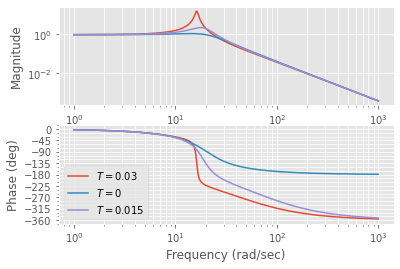
Anders als im ersten Fall ist der gleiche Regler \(-1\) für die Parameterschwankungen hier nicht geeignet. Die Einfachste Lösungen wäre den Regler weniger aggressiv auszulegen d.h. zum Beispiel eine Reglerverstärkung von \(-0.1\) zu verwenden. Für kleine Parameterschwankungen hat sich das Feld der robusten Regelungstechnik entwickelt welches solche Fragestellungen adressiert. Für große Parameterschwankungen muss auf die adaptive Regelungstechnik ausgewichen werden.
Fazit
Für das Beurteilen offener Regelkreise sind Bode-Diagramme geeigneter als Systemantworten im Zeitbereich. Die Übergangsfrequenz des geschlossenen Regelkreises ist eine entscheidende Größe für den Regelentwurf.
Obwohl es der Intuition widersprich, ist ein Übergang von stabilen zu instabilen Dynamiken nicht immer ein Problem für den Reglerentwurf. Im ersten Beispiel führt der gleiche Regler für alle 3 System zu sehr ähnlichen Systemantworten.
Umgekehrt können Parameterschwankungen das Verhalten des geschlossenen Systems sehr stark beeinflussen, obwohl der Effekt im offenen Regelkreis nicht signifikant erscheinen mag.
Schon lineare einschleifige System weisen ein sehr komplexes Verhalten auf. In der Realität kommen meist Störungen, Totzeiten, zeitvariante Effekte, Mehrgrößen-Eingänge und Zustandsverkopplungen oder nichtlineares Verhalten hinzu. Das alles macht das Feld der Kybernetik extrem anspruchsvoll aber auch sehr interessant.
Referenzen
- Wikipedia: Robuste Regelung
- Wikipedia: Apdative Regelung
- Adaptive Control, Second Editon, Karl J. Aström, Björn Wittenmark