Slycot - Einführung

Einige Methoden von Python-Control basieren auf der Fortran-Bibliothek SLICOT, welche in dem Python Modul Slycot verpackt sind.

Python-Control gliedert sich also in drei Teile:

SLICOT - Ein Fortran 77 Bibliothek
Slycot - Ein Wrapper um SLICOT
Python-Control - Python Bibliothek

SLICOT - Subroutine Library in Systems and Control Theory

Die Subroutinenbibliothek SLICOT bietet Fortran 77-Implementierungen numerischer Algorithmen für Berechnungen in der System- und Regelungstheorie. Basierend auf Routinen der numerischen linearen Algebra aus BLAS- und LAPACK-Bibliotheken bietet SLICOT Methoden für den Entwurf und die Analyse von Steuerungssystemen.

Die aktuelle Version von SLICOT besteht aus über 600 vom Benutzer aufrufbaren Routinen. Der SLICOT Kern zielt auf die Wiederverwendbarkeit der Routinen in verschiedenen Sprachen. So werden einige Routinen von Projekten in Matlab, Octave, Scilab, R, Julia oder Python verwendet.

Nachteilig ist, dass der Fortran 77 Standard für moderne Augen schwer zu lesen ist. Mithilfe des Slycot Paketes können wir jedoch auf gewisse Methoden zugreifen und uns so auch indirekt mit den SLICOT Routinen vertraut machen. Einerseits können wir so Algorithmen besser verstehen, andererseits auch das Python-Control Projekt besser kennenlernen.

Die SLICOT-Bibliothek ist nach Kapiteln organisiert. Jedes Kapitel kann durch einen einzelnen Buchstaben identifiziert werden. Folgende Kapitel sind enthalten:

A: Analyseroutinen
B: Benchmark- und Testprobleme
C: Adaptive Control (derzeit leer)
D: Datenanalyse
F: Filtern
I: Identifikation
M: Mathematische Routinen
N: Nichtlineare Systeme
S: Syntheseroutinen
T: Transformationsroutinen
U: nützliche Routinen

Die Dokumentation von SLICOT ist online verfügbar. Es enthält die vollständigen Beschreibungen aller verfügbaren Subroutinen.

Slycot - Methods

Derzeit stehen bei weitem nicht alle SLICOT Methoden in Slycot zur Verfügung. Wir können die Methoden unter der Zuhilfenahme von Regular expression und dem Befehl dir() herausfiltern.

import re
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

import slycot
slycot.__version__

'0.5.0.0'

In der Textdatei slicot_methods.txt sind alle Routinen der SLICOT Bibliothek aufgelistet.

with open('slicot_methods.txt') as f:
    lines = f.readlines()

slicot_methods = [x.split("\n")[0] for x in lines]

print(slicot_methods)
print(f"Derzeit in Slicot {len(slicot_methods)} Routinen implementiert.")

['mb01wd', 'tg01gd', 'ab13fd', 'sg03ay', 'mb01oe', 'mb02fd', 'tg01oa', 'dg01ny', 'sg03ax', 'fb01qd', 'ma02az', 'mc01md', 'md03by', 'tf01mx', 'ib01nd', 'mb02rz', 'mb04bp', 'tb01kd', 'ab09gd', 'ma02jz', 'ud01cd', 'ib01rd', 'nf01bx', 'mb02rd', 'ma02es', 'mb04iy', 'tg01id', 'mb01rd', 'mc01xd', 'mb04wr', 'sg03bs', 'mb03kc', 'ma02cd', 'tb04ad', 'md03bx', 'mb03vy', 'ab09cd', 'tf01nd', 'sb09md', 'sb03ot', 'mb04pu', 'mb04yd', 'mb02pd', 'mb04tu', 'mb02ud', 'ib01cd', 'mb04dp', 'tg01fz', 'sb04od', 'nf01ad', 'mb03qd', 'ab09bd', 'mb02jd', 'sb02mw', 'ma02ad', 'mb04dl', 'sb08ed', 'tb01uy', 'md03ba', 'ab05nd', 'mb03pd', 'sb02mx', 'sb04ow', 'ma02mz', 'mb02cy', 'ag08by', 'mb03bb', 'ab09cx', 'mb01kd', 'sb02sd', 'mb01xd', 'sb01md', 'mb02ny', 'sb02ox', 'sb10pd', 'ma01cd', 'tg01hd', 'mb02nd', 'sb02cx', 'sb04px', 'mb03qg', 'tg01hx', 'mb03ag', 'mc01py', 'mb03kb', 'mb04jd', 'tg01bd', 'tb03ay', 'ab13ed', 'sb03rd', 'ma02id', 'ma02md', 'sb03os', 'mb02cv', 'mb05oy', 'sb06nd', 'nf01bp', 'sb02od', 'mb03md', 'fb01vd', 'ma02iz', 'tb01ld', 'mb02sd', 'tb01nd', 'ud01md', 'mb02xd', 'mb02md', 'sg03br', 'mb04az', 'sb02ru', 'sb10qd', 'sg03bu', 'sb04qr', 'mb03lf', 'ma01ad', 'sb04rd', 'ma02gd', 'sb04ry', 'ab13ad', 'ab13md', 'nf01by', 'mb04nd', 'mb03yt', 'sg02cx', 'tg01hu', 'ab09kx', 'mb04hd', 'mb03gd', 'sb08cd', 'mb03od', 'sb04mr', 'mb02kd', 'ab09jx', 'ud01bd', 'fb01sd', 'mb03rd', 'ab07nd', 'mb03fd', 'sb03ou', 'mb03ya', 'mb01rh', 'sb08hd', 'ab08nw', 'ab07md', 'ab05qd', 'mb02qy', 'mb03id', 'ma02bd', 'ma02dd', 'mb04ed', 'sb03td', 'mb04tv', 'td04ad', 'tb01ud', 'tc01od', 'nf01bs', 'ma02oz', 'sg02nd', 'mb04ru', 'mc01rd', 'mb03bd', 'mb04tt', 'sb08ny', 'tg01ad', 'sb04qu', 'nf01bf', 'tg01qd', 'mc01td', 'mb04fp', 'mb03ud', 'mb3lzp', 'sb04nv', 'mb04qb', 'mb04wp', 'mc01sy', 'sb10dd', 'mb02sz', 'mb04kd', 'tb04bw', 'mb01ry', 'sb03mv', 'tb03ad', 'mb03gz', 'mb01ot', 'mb03be', 'tb01zd', 'ab04md', 'mb01os', 'sb03qx', 'mb04pb', 'nf01bu', 'mb04su', 'mc01od', 'sb16bd', 'mb02td', 'sg03ad', 'sb03qy', 'mb03xs', 'md03bb', 'mb04qc', 'mb03jd', 'sb01by', 'ab09nd', 'sb03md', 'mb04oy', 'mb05nd', 'ab08nx', 'mb01rb', 'dg01md', 'mb02wd', 'sb03ud', 'mb03py', 'mc01pd', 'ma02pz', 'ab09iy', 'ma02od', 'sb10td', 'tf01my', 'sb16cy', 'tg01oz', 'ab05pd', 'mb04cd', 'sb16ay', 'sb10hd', 'mb02gd', 'mc03md', 'mb03bc', 'sb04nx', 'mc01qd', 'ab01od', 'ab09jd', 'sb16ad', 'sg03bv', 'nf01bb', 'ab09dd', 'mb03lp', 'md03bf', 'mb03ah', 'mb3jzp', 'sb04mu', 'ab09kd', 'sb03ov', 'sb03pd', 'fd01ad', 'sb03sd', 'td05ad', 'mb02hd', 'mb02cd', 'mb03qx', 'sb04nd', 'mb04tb', 'sb04pd', 'tg01jy', 'tb04cd', 'tg01dd', 'ab09ed', 'mb03wx', 'tg01pd', 'tf01pd', 'sb08fd', 'ab13ax', 'nf01ba', 'sb08md', 'mb04dy', 'sb04my', 'ab09fd', 'mb04vd', 'mb01md', 'ib01oy', 'mb04ld', 'sb01bd', 'sb02mu', 'sg03bx', 'tg01ed', 'mb02qd', 'mb01ss', 'mb01rw', 'sb10ud', 'mb03cz', 'ag8byz', 'sb02ow', 'mb02dd', 'sb08nd', 'mb03my', 'mb03yd', 'tg01od', 'mc01sw', 'ma02bz', 'ib01ad', 'ab09hd', 'ud01mz', 'td03ad', 'sb03my', 'ib03bd', 'mb04dd', 'mb04xd', 'ma02hd', 'ab09ax', 'tg01hy', 'mc01sx', 'tb01ux', 'df01md', 'mb04vx', 'mb04wd', 'ab08md', 'tb01vd', 'nf01ay', 'md03bd', 'mb03rz', 'ab09ix', 'ab13dd', 'tb01iz', 'nf01bw', 'mb04qf', 'ab05sd', 'mb04db', 'mb03ai', 'sb08gd', 'mb02od', 'mb04ty', 'mb02uv', 'ib01px', 'tb01ty', 'sb03oy', 'sb03mu', 'tg01nd', 'ab09hx', 'ab09id', 'mb04id', 'mb03ed', 'mb04di', 'mb04tx', 'sb03od', 'mb04xy', 'mb03hz', 'tc04ad', 'mb01rx', 'sb02ov', 'mb03zd', 'mb03jp', 'mb02yd', 'mb04ox', 'bd01ad', 'mb04fd', 'ab05md', 'tb04bx', 'dg01od', 'sb10zd', 'mb01rt', 'sb02mr', 'ab01nd', 'mb04bz', 'ma01bz', 'ma02ed', 'mb03ld', 'tb01md', 'tb01xz', 'mb04qs', 'ab09md', 'sb10id', 'sb03sx', 'mb02cu', 'ab13bd', 'mb3oyz', 'mb02tz', 'tb01px', 'mb03iz', 'sg03bw', 'mb04dz', 'nf01bv', 'bd02ad', 'tf01md', 'mb03wd', 'mb4dbz', 'mb04tw', 'mb03vd', 'mb01oo', 'fb01rd', 'mb04rb', 'mb03ry', 'mb01xy', 'tb05ad', 'ib03ad', 'mb03xz', 'mb05md', 'mb02ed', 'sb03mw', 'sg03bd', 'mb01ru', 'mb01oc', 'bb02ad', 'ab09jw', 'mb03cd', 'mb04pa', 'sb10yd', 'mb02jx', 'tg01az', 'sg02ad', 'ma02hz', 'mb03dz', 'tg01md', 'sb08my', 'tb04ay', 'sb02nd', 'sb02mt', 'sb04rw', 'mb04wu', 'nf01be', 'de01pd', 'sb02mv', 'sb10ed', 'sb10zp', 'mb03lz', 'sb02oy', 'sb04md', 'mb03bg', 'mb03ad', 'mb01uw', 'sb10kd', 'ma02jd', 'ma02gz', 'tf01qd', 'mb03td', 'mb04gd', 'tb04bv', 'tg01ld', 'mb03ba', 'ue01md', 'mb3pyz', 'mb03xp', 'sb02ou', 'mb01nd', 'sg02cw', 'mb04yw', 'sb04mw', 'mb01uy', 'sg03by', 'ib01py', 'mb02uw', 'tg01ob', 'mb03jz', 'mb04ad', 'tg01fd', 'mb03sd', 'ab13id', 'ab08ny', 'mb03za', 'mb02uu', 'ab08nd', 'mc01wd', 'tg01ly', 'mb01uz', 'mb03xu', 'mb03nd', 'ag07bd', 'sg03bt', 'mb03xd', 'ma02nz', 'ab13dx', 'ab08nz', 'sb04ny', 'mb03ts', 'sb04qy', 'mb03rx', 'mb03af', 'ib01md', 'mb03ke', 'sb02pd', 'sb16cd', 'ab8nxz', 'mb04bd', 'tf01rd', 'mb01ux', 'mb03bz', 'sb03sy', 'mc03ny', 'sb10ld', 'ma02fd', 'td03ay', 'bb04ad', 'mb03ab', 'dk01md', 'ab05od', 'mc03nx', 'mb01td', 'tb01id', 'tg01cd', 'mb04ow', 'sb04nw', 'mb03ae', 'mb03rw', 'mb03qy', 'sb04py', 'nf01bq', 'mb03dd', 'tb01kx', 'mb01ud', 'ma01bd', 'mb03ny', 'ab08mz', 'sb02rd', 'sb04qd', 'tb01wx', 'ag08bz', 'tg01wd', 'tb04bd', 'sb02md', 'bb01ad', 'mc01sd', 'mc01vd', 'sb10ad', 'mb01vd', 'de01od', 'ib01pd', 'mb03bf', 'sb02ms', 'mb04py', 'mc03nd', 'tb01wd', 'mc01nd', 'dg01nd', 'ab09ad', 'mb02id', 'tb01yd', 'sb03mx', 'mb03vw', 'sg02cv', 'ab05rd', 'mb04ds', 'mb01od', 'mb4dpz', 'mb03oy', 'sb03qd', 'sb01bx', 'sb08dd', 'ib01od', 'sb10md', 'mb01ld', 'mb04iz', 'mb05od', 'tb01td', 'mb02vd', 'mb03fz', 'mb05my', 'mb01oh', 'mb04zd', 'sb03oz', 'tg01kz', 'mb02cx', 'tg01jd', 'mb01zd', 'mb01pd', 'sb01dd', 'mb03hd', 'sb02qd', 'mb03qw', 'tb01xd', 'ud01nd', 'sb10rd', 'ib01my', 'tf01od', 'ud01dd', 'tb01vy', 'ab09hy', 'sb04rx', 'ib01qd', 'mb04od', 'mb03qv', 'sg03bz', 'sb03or', 'mb03kd', 'ab13cd', 'tg01kd', 'mb03wa', 'mb04ts', 'mb03ka', 'mb4dlz', 'mb04qu', 'sb10fd', 'ma02pd', 'sb10jd', 'mb01qd', 'ab09jv', 'sb10vd', 'fb01td', 'ma02ez', 'tc05ad', 'sb10wd', 'md03ad', 'nf01bd', 'ma02cz', 'mb04ny', 'sb04rv', 'nf01br', 'tb01pd', 'ab01md', 'ib01bd', 'mb01yd', 'tg01nx', 'sb01fy', 'mb04md', 'sb10sd', 'mb04ud', 'mb01sd', 'ag08bd', 'ab09bx', 'bb03ad']
Derzeit in Slicot 607 Routinen implementiert.

def get_slycot_method(sly):
    can_methods = dir(sly)
    r = re.compile("[a-z][a-z][0-9][0-9a-z][a-z][a-z]")
    slycot_methods = list(filter(r.match, can_methods)) # Read Note below
    return slycot_methods

slycot_methods = get_slycot_method(slycot)

print(slycot_methods)
print(f"Derzeit in Slycot {len(slycot_methods)} Methoden implementiert.")

['ab01nd', 'ab05md', 'ab05nd', 'ab07nd', 'ab08nd', 'ab08nz', 'ab09ad', 'ab09ax', 'ab09bd', 'ab09md', 'ab09nd', 'ab13bd', 'ab13dd', 'ab13ed', 'ab13fd', 'ab13md', 'mb03rd', 'mb03vd', 'mb03vy', 'mb03wd', 'mb05md', 'mb05nd', 'mc01td', 'sb01bd', 'sb02md', 'sb02mt', 'sb02od', 'sb03md', 'sb03md57', 'sb03od', 'sb04md', 'sb04qd', 'sb10ad', 'sb10dd', 'sb10fd', 'sb10hd', 'sg02ad', 'sg03ad', 'sg03bd', 'tb01id', 'tb01pd', 'tb03ad', 'tb04ad', 'tb05ad', 'tc01od', 'tc04ad', 'td04ad', 'tf01md', 'tf01rd']
Derzeit in Slycot 49 Methoden implementiert.

def count_methods(list_methods):
    d = {}
    for w in list_methods:
        if w:
            if w[0] in d:
                d[w[0]] = d[w[0]] + 1
            else:
                d[w[0]] = 1
    return d

slicot_methods_count = count_methods(slicot_methods)
slycot_methods_count = count_methods(slycot_methods)
print(f"{slicot_methods_count = }")
print(f"{slycot_methods_count = }")

slicot_methods_count = {'m': 281, 't': 77, 'a': 60, 's': 131, 'd': 8, 'f': 6, 'i': 15, 'u': 7, 'n': 16, 'b': 6}
slycot_methods_count = {'a': 16, 'm': 7, 's': 16, 't': 10}

slicot_full_names = {
    "a": "Analysis Routines",
    "b": "Benchmark",
    "c": "Adaptive Control",
    "d": "Data Analysis",
    "f": "Filtering",
    "i": "Identification",
    "m": "Mathematical routines",
    "n": "Nonlinear Systems",
    "s": "Synthesis Routines",
    "t": "Transformation Routines",
    "u": "Utility Routines",
}

names_sli = list(slicot_methods_count.keys())
values_sli = list(slicot_methods_count.values())

names_sly = list(slycot_methods_count.keys())
values_sly = list(slycot_methods_count.values())


plt.barh(range(len(slicot_methods_count)), values_sli, tick_label=[slicot_full_names[x] for x in names_sli])
plt.barh(range(len(slycot_methods_count)), values_sly)
plt.legend(("slicot","slycot"))
plt.title("Slicot vs Slycot")
plt.show()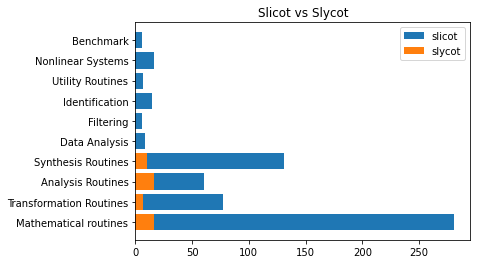

print(f"Folgende Methoden sind nur in Slyot und nicht in Slicot vorhanden: {set(slycot_methods) - set(slicot_methods)}")

Folgende Methoden sind nur in Slyot und nicht in Slicot vorhanden: {'sb03md57'}

print(f"Derzeit sind in Slycot {len(slycot_methods)} Methoden und in Slicot {len(slicot_methods)} implementiert.")
print(f"D.h es sind {(len(slycot_methods)-1)/len(slicot_methods)*100} % der SLICOT Routinen in Slycot vorhanden, wobei die obige Methode {set(slycot_methods) - set(slicot_methods)} abgezogen ist.")

Derzeit sind in Slycot 49 Methoden und in Slicot 607 implementiert.
D.h es sind 7.907742998352553 % der SLICOT Routinen in Slycot vorhanden, wobei die obige Methode {'sb03md57'} abgezogen ist.

Näherungsweise sind also weniger als 10 % der SLICOT Routinen in Slycot verpackt. Umgekehrt zeigt diese Untersuchung, welches Potenzial für Python-Control noch vorhanden ist.

Slycot: \(\mathcal{H}_2\) - Norm

In einem früheren Blogeintrag haben wir die \(\mathcal{H}_2\)-Norm für zeitdiskrete Systeme besprochen. Eine Textsuche in der SLICOT Dokumentation liefert die Routine ab13bd als jene, mit der wir die \(\mathcal{H}_2\)-Norm berechnen können.

Slycot: ab13bd

def check_in_slycot(method, sly):
    slycot_methods = get_slycot_method(sly)
    return method in slycot_methods

check_in_slycot('ab13bd',slycot)

True

Die help() Methode erlaubt uns das Studieren der Dokumentation. Wie wir sehen, müssen wir eine ganze Reihe an Parametern an die Methode übergeben. Ein Zweck des Python-Control Projekts ist es, eine einfachere Schnittstelle für den Benutzer bereitzustellen. Dadurch ist weniger Wissen über die Algorithmen notwendig.

help(slycot.ab13bd)

Help on function ab13bd in module slycot.analysis:

ab13bd(dico, jobn, n, m, p, A, B, C, D, tol=0.0)
    norm = ab13bd(dico, jobn, n, m, p, A, B, C, D, [tol])
    
    To compute the H2 or L2 norm of the transfer-function matrix G
    of the system (A,B,C,D). G must not have poles on the imaginary
    axis, for a continuous-time system, or on the unit circle, for
    a discrete-time system. If the H2-norm is computed, the system
    must be stable.
    
    Parameters
    ----------
    dico : {'D', 'C'}
        Indicate whether the system is discrete 'D' or continuous 'C'.
    jobn : {'H', 'L'}
        H2-norm 'H' or L2-norm 'L' to be computed.
    n : int
        The number of state variables.  n >= 0.
    m : int
        The number of system inputs.  m >= 0.
    p : int
        The number of system outputs.  p >= 0.
    A : (n,n) ndarray
        The leading n-by-n part of this array must contain the state
        dynamics matrix A of the system.
    B : (n,m) ndarray
        The leading n-by-m part of this array must contain the input/state
        matrix B of the system.
    C : (p,n) ndarray
        The leading p-by-n part of this array must contain the state/output
        matrix C of the system.
    D : (p,m) ndarray
        The leading p-by-m part of this array must contain the direct
        transmission matrix D of the system.
    tol : float, optional
        The absolute tolerance level below which the elements of
        B are considered zero (used for controllability tests).
        If the user sets tol <= 0, then an implicitly computed,
        default tolerance, defined by  toldef = n*eps*norm(B),
        is used instead, where eps is the machine precision
        (see LAPACK Library routine DLAMCH) and norm(B) denotes
        the 1-norm of B.
    
    Returns
    -------
    norm:  H2 or L2 norm of the system (A,B,C,D)
    
    Raises
    ------
    SlycotArithmeticError
        :info == 1:
            The reduction of A to a real Schur form failed
        :info == 2:
            A failure was detected during the reordering of the
            real Schur form of A, or in the iterative process for
            reordering the eigenvalues of `` Z'*(A + B*F)*Z`` along the
            diagonal (see SLICOT routine SB08DD)
        :info == 3 and dico == 'C':
            The matrix A has a controllable eigenvalue on the imaginary axis
        :info == 3 and dico == 'D':
            The matrix A has a controllable eigenvalue on the unit circle
        :info == 4:
            The solution of Lyapunov equation failed because the
            equation is singular
        :info == 5:
            D is a nonzero matrix
        :info == 6:
            The system is unstable
    
    Warns
    -----
    SlycotResultWarning
        :iwarn > 0:
            {iwarn} violations of the numerical stability condition
            occured during the assignment of eigenvalues in
            computing the right coprime factorization with inner
            denominator of `G` (see the SLICOT subroutine SB08DD).

import numpy as np
import scipy.linalg as linalg

Ad_stable = np.array([[0.5, 0.1],[0.1, 0.5]])

Bd = np.array([[0.],[1.]])
Cd = np.eye(2)
Dd = np.zeros((2,1))

dico = 'D'
jobn = 'H'
n = 2
m = 1
p = 2

h2norm_d_slycot = slycot.ab13bd(dico, jobn, n, m, p, Ad_stable, Bd, Cd, Dd)
h2norm_d_slycot

1.1732382943111324

Die \(\mathcal{H}_2\) - Norm beträg also 1.1732382943111324.

Verleich mit ‘scipy’

Wir wollen nun eine alternative Implementierung basierend auf SciPy verwenden, wie wir sie in dem Blogeintrag

H2-Norm linearer zeitdiskreter zeitinvarianter Systeme (d-LTI)

hergeleitet haben.

Warnung

Da sich die obige Slycot Methode und die untere Scipy Methode aus nicht ganz ersichtlichen Gründen beeinflussen, wollen wir das Jupyter Notebook mit %reset -f neu starten. Der Grund liegt wahrscheinlich in einer LAPACK oder BLAS Variable, welche im Notebook gespeichert wird, und sowohl in der Slycot Methode als auch in der Scipy Methode verwendet wird.

%reset -f

import warnings
warnings.filterwarnings("error")

import numpy as np
import scipy.linalg as linalg


Ad_stable = np.array([[0.5, 0.1],[0.1, 0.5]])
Bd = np.array([[0.],[1.]])
Cd = np.eye(2)
Dd = np.zeros((2,1))

def h2norm_d(A,B,C,D):
    """ naive implementation of the h2 system norm of linear time-discrete time-invariant systems (d-LTI)
        (there might be better ways to do that, => check papers)
    """
    try:
        P = linalg.solve_discrete_lyapunov(A.T, B@B.T)
        if np.all(np.real(linalg.eigvals(P)) < 0):
            H2 = np.inf
        else:
            H2 = np.sqrt(np.trace(C@P@C.T+D@D.T))
    except RuntimeWarning:
        H2 = np.inf
    return H2

h2norm_d_scipy = h2norm_d(Ad_stable,Bd,Cd,Dd)
h2norm_d_scipy

1.1732382943111324

Wir erhalten also dasselbe Ergebnis wie mit der Slycot Methode. Der Aufruf der Slycot Methode ist zwar etwas komplizierter, jedoch sind diese Algorithmen eigenen Implementierungen vorzuziehen.

Fazit

SLICOT bietet noch sehr viel Potenzial für Python-Control. Viele Routinen können noch in Slycot Methoden verpackt werden, womit fortschrittlichere Algorithmen in Python verfügbar würden. Die Weiterentwicklung der SLICOT - Fortran 77 Bibliothek ist jedoch nicht ganz sichergestellt. Eine Umstellung auf einen neueren Fortran Standard wie etwa Fortran 2018 oder Fortran 2023 könnte dem Projekt neues Leben einhauchen. Fortran wird derzeit sehr stark weiterentwickelt.