PI-Regler Tuning ~ Åström-Hägglund

In ihrem Buch Advanced PID Control haben Åström und Hägglund ein verbessertes Tuning für PI-Regler vorgestellt. Wie beim Ziegler-Nichols stehen Tuning-Tabellen für den Zeitbereich als auch den Frequenzbereich zur Verfügung.

Zeitbereich

Auf Basis eines FOPTD Modells \((K,T,L)\) schlagen Åström und Hägglund folgende PI-Parametrierung vor:

Reglertyp	\(K_p\)	\(K_i\)
Aström-Hägglund PI	\(\frac{0.15L+0.35T}{KL}\)	\(\frac{0.46L+0.02T}{KL^2}\)
Ziegler-Nichols PI	\(\frac{0.9T}{KL}\)	\(\frac{0.27T}{KL^2}\)

Frequenzbereich

Auch auf Basis der Frequenzbereichs-Parameter \(k_c, w_c, (K)\) werden von Aström und Hägglund folgende PI-Parameter vorgeschlagen. Dieses Tuning erfordert aber einen weiteren Parameter \(K\), welcher die konstante Verstärkung der Strecke darstellt.

Reglertyp	\(K_p\)	\(K_i\)
Aström-Hägglund PI	\(0.16k_c\)	\(\frac{0.16k_c+0.072/K}{T_c}\)
Ziegler-Nichols PI	\(0.45k_c\)	\(\frac{0.54k_c}{T_c}\)

Hinweis: Das Åström-Hägglund Tuning liefert meist niedrigere Reglerverstärkungen als die Ziegler-Nichols Methode. Es sei noch darauf hingewiesen, dass die hier verwendete PI-Reglerstruktur eine parallele Struktur ist. Wir könnten die \(K_p\) und \(K_i\) Werte aber auf die \(K_p\) und \(T_i = K_p / K_i\) Werte umrechnen.

Beispiel

Mit diesem Beispiel wollen wir zeigen, dass modifizierte Einstellregeln oft bessere Ergebnisse liefern, als die ursprüngliche Ziegler-Nichols Methode. Ist ein Modell gegeben, so erweisen sich gerade die Frequenzbereichsmethoden als einfach anzuwenden.

Gegeben sei die Strecke (Rasterkraftmikroskop)

\[ P(s) = \frac{1-e^{-sT_n}}{sT_n(s+1)} \]

wobei für \(T_n = 2n\pi a/\omega_0 = 2n\pi\xi\). Für dieses Beispiel legen wir die Parameter mit \(\xi=0.002\) und \(n=20\) fest.

import numpy as np
import matplotlib.pyplot as plt
plt.style.use('ggplot')

import control as ct

s = ct.tf('s')

n = 20
xi = 0.002 
Tn = 2*n*np.pi*xi

num, den  = ct.pade(Tn,4)
P = ct.minreal((s/s-ct.tf(num,den))/(s*Tn*(s+1)))
P

2 states have been removed from the model

\[\frac{633.3 s^2 + 4.211 \times 10^{5}}{s^5 + 80.58 s^4 + 2929 s^3 + 5.576 \times 10^{4} s^2 + 4.74 \times 10^{5} s + 4.211 \times 10^{5}}\]

Die Verstärkung \(K=P(0)\) kann mit der Methode control.gcgain oder mit der Methode ct.freqresp ermittelt werden.

K = ct.dcgain(P)
print(f"Die Verstärkung der Strecke lautet {K}.")
np.allclose(ct.dcgain(P),ct.freqresp(P,0)[0][0])

Die Verstärkung der Strecke lautet 0.9999999999999978.

True

gm, pm, wg, wp = ct.margin(P)
kc = gm
wc = wg
Tc = 2*np.pi/wc
print("Kritische Verstärkung", kc)
print("Kritische Frequenz", wc)
print("Kritische Periodenzeit", Tc)

Kritische Verstärkung 21.726882224637702
Kritische Frequenz 13.110950964797556
Kritische Periodenzeit 0.4792318516063189

def astrom_hagglund(kc,Tc,K):
    kp = kc*0.16
    ki = (0.16*kc+0.72/K)/(Tc)
    return kp, ki

def ziegler_nichols(kc,Tc):
    kp = kc*0.45
    #Ti = Tc/1.2
    ki = 0.54*kc/Tc
    return kp, ki

kp, ki = ziegler_nichols(kc,Tc)
print(f" Die Reglerverstärkungen ergeben sich mit der Ziegler-Nichols Methode zu {kp = } und {ki = }.")
C_1 = kp+ki/s
kp, ki = astrom_hagglund(kc,Tc,K)
print(f" Die Reglerverstärkungen ergeben sich mit der Aström-Hägglund Methode zu {kp = } und {ki = }.")
C_2 = kp+ki/s

 Die Reglerverstärkungen ergeben sich mit der Ziegler-Nichols Methode zu kp = 9.777097001086966 und ki = 24.48192114522143.
 Die Reglerverstärkungen ergeben sich mit der Aström-Hägglund Methode zu kp = 3.4763011559420325 und ki = 8.756306872918845.

Das verbesserte Verfahren nach Åström und Hägglund liefert kleinere Reglerparameter und der PI-Regler ist somit als weniger aggressiv anzusehen.

L_1 = ct.minreal(P*C_1)
T_1 = ct.feedback(L_1,1)
_,_,gs,_,_,ws = ct.stability_margins(L_1)
print(f"Die Stabilitätsreserve tritt bei {ws = } rad/s auf und nimmt den Wert {gs = } an.")
L_2 = ct.minreal(P*C_2)
T_2 = ct.feedback(L_2,1)
_,_,gs,_,_,ws = ct.stability_margins(L_2)
print(f"Die Stabilitätsreserve tritt bei {ws = } rad/s auf und nimmt den Wert {gs = } an.")

0 states have been removed from the model
Die Stabilitätsreserve tritt bei ws = 9.487327421223707 rad/s auf und nimmt den Wert gs = 0.2685244048683104 an.
0 states have been removed from the model
Die Stabilitätsreserve tritt bei ws = 5.7624674998827174 rad/s auf und nimmt den Wert gs = 0.6139198817877397 an.

Der PI-Regler nach Åström und Hägglund besitzt eine größere Stabilitätsreserve und ist somit weniger empfindlich gegenüber Parameter-Schwankungen der Strecke. Diese größere Stabilitätsreserve ist mithilfe des Nyquist-Diagramms deutlich zu erkennen.

plt.figure(figsize=(16,8))
ct.nyquist([P,L_1,L_2])
circle1 = plt.Circle((0, 0), 1., color='black', fill=False)
plt.gca().add_patch(circle1)
plt.ylim([-3,3])
plt.xlim([-3,3])
plt.gca().set_aspect('equal', 'box')

# for legend
lines = plt.gca().get_lines()
legend = plt.legend([lines[i] for i in [0,3,6]], ["Prozess", "Ziegler-Nichols", "Aström-Hägglund"], loc=1)
plt.gca().add_artist(legend)

plt.show()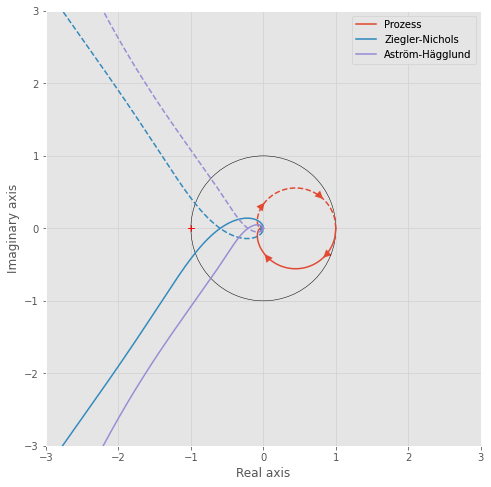

plt.figure(figsize=(16,8))
tout, yout = ct.step_response(T_1, 10)
plt.plot(tout, yout, label='Ziegler-Nichols')
tout, yout = ct.step_response(T_2, 10)
plt.plot(tout, yout, label='Aström-Hägglund')
plt.legend()
plt.show()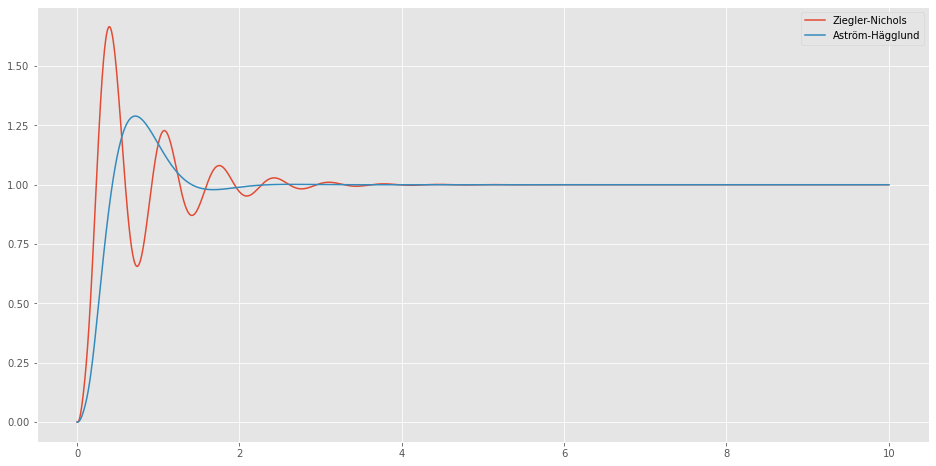

Fazit

Wir sehen, dass das verbesserte Verfahren nach Åström-Hägglund einen weniger aggressiven und robusteren PI-Regler erzeugt.

Die bekannten Tuning-Verfahren wie Ziegler-Nichols und Chien-Hrones-Reswick liefern oftmals nicht die besten PID-Regler. Es kann hilfreich sein, mit verschiedenen PID-Tuning-Verfahren vertraut zu sein.

Referenzen

Feedback Systems: An Introduction for Scientists and Engineers, Second Edition, 2020/2022 (Karl J. Aström, Richard M. Murray)
PID Controllers: Theory, Design and Tuning, Second Edition, 1995 (Karl J. Åström, Tore Hägglund)
Advanced PID Control, 2006 (Karl J. Åström, Tore Hägglund)