100 Jahre PID und 80 Jahre Ziegler-Nichols

Kybernetik
Regelungstechnik
Autor:in

Johannes Kaisinger

Veröffentlichungsdatum

21. Februar 2022

Dieses Jahr (2022) feiern wir 100 PID-Regelung auf einer wissenschaftlichen Grundlage. Der erste mathematische fundierte wissenschaftliche Aufsatz wurde 1922 von Nicolas Minorsky veröffentlicht.

Auch die berühmten Einstellstellregeln nach Ziegler-Nichols haben einen runden Geburtstag und wurden 20 Jahre später 1942 vorgestellt.

Kurze Geschichte des PID Reglers

Die Geschichte der Regelungstechnik ist sehr umfangreich, lässt sich bis in die Antike zurückverfolgen, und ist ursprünglich eng mit dem Problem der Zeitmessung verbunden. Erste Regelungskonzepte sind in den Wassermechanismen und Wasseruhren der Griechen, Araber und Perser zu finden. Der Wasserstandsregler nach Ktesibios aus Alexandria (ca. 300 v.C.) gilt als erste belegte Anwendung der Regelungstechnik.

Das Geburtsjahr des PID-Reglers wird in der Literatur mit 1911 angegeben und ist mit dem Namen Elmer Sperry verbunden. Sperry verwendetet einen PID-Regler zur Automatisierung eines Schiffssteuermechanismus.

Im Jahr 1922 legte Nicolas Minorsky den ersten wissenschaftlichen Aufsatz mit dem Titel “Directional stability of automatically steered bodies” vor. Er verwendete den Begriff 3 Term Regler. 1935 zeigt S.D. Mitereff erstmals eine Zeitbereichsdarstellung im Paper “Principles underlying the rational solution of automatic-control problems” und führte die Begriffe P, PI, PD, PID ein.

Kurze Geschichte der Faustformeln

Obwohl sich PID-Regler in den 1920er und 1930er Jahren sehr schnell in verschiedenen Industrien ausbreiteten, stellte sich schon bald die Frage wie die 3 Parameter eingestellt werden sollten. Je nach Anwendungsfeld können sich die Werte sehr stark unterscheiden. Falsch eingestellte Regler führen immer zu ungewünschten Ergebnissen und können sogar die Zerstörung der Maschine bewirken.

Oft werden die Einstellregeln nach Ziegler-Nichols als erste Tuning-Verfahren bezeichnet. Folgt man aber Aidan O’Dwyer, so haben Albert Callander et. al schon 1934, also 6 Jahre früher, die ersten Faustformeln präsentiert. Der interne Report der Firma Imperial Chemical Industieres (ICI), trägt den Titel “Preliminary notes in automatic control”. In den Jahren 1935/36/37 folgten weiter Veröffentlichungen.

Die Einstellregeln nach Ziegler-Nichols wurden 1942 vorgestellt und haben ein großer Bekanntheit erlangt. Das Orginal-Paper trägt den Namen “Optimum Settings for Automatic Controllers”. Jeder Regelungstechniker bekommt diese Faustformeln in seiner Ausbildung präsentiert.

Ziegler-Nichols

Wir wollen die Ziegler-Nichols Methode in einer etwas moderneren Form besprechen. Grundsätzlich gibt es zwei Settings. Das erste Verfahren basiert auf Charakteristiken der Sprungantwort des Systems, das zweite Verfahren basiert auf dem sogenannten Schwingversuch eines geschlossenen Regelkreises.

Abbildung 1: Ziegler-Nichols Tuning

Ziegler Nichols, CheatSheet

Offener Regelkreis (Sprungantwort)

In der modernen Form ist sowohl ein empirisches Vorgehen als auch ein modellbasiertes Vorgehen möglich. Die Strecke wird als nicht schwingungsfähig angenommen.

Empirisches Vorgehen

Für das empirische Vorgehen wird das System mit einem Sprung angeregt. Die Sprungantwort wird mithilfe der Wendetangente charakterisiert, welche eindeutig durch die Parameter \(a\) und \(L\) bestimmt ist. Es sei ausdrücklich darauf hingewiesen, dass der stationäre Punkt nicht erreicht werden muss, um dieses Verfahren anzuwenden.

Die PID Parameter können dann aus der Tabelle

Reglertyp \(K_p\) \(T_i\) \(T_d\)
\(P\) \(1/a\) \(-\) \(-\)
\(PI\) \(0.9/a\) \(3L\) \(-\)
\(PID\) \(1.2/a\) \(4L\) \(L/2\)

entnommen werden.

Modellbasiertes Vorgehen

Das modellbasierte Vorgehen basiert auf einer Modellreduktion. Gegeben sein eine Übertragungsfunktion der Form

\[ G(s) = \frac{b_m s^m + b_{m-1}s^{m-1}+\cdots+b_0}{a_n s^n + a_{n-1}s^{n-1}+\cdots+a_0}e^{-sL} \]

welche auf das Modell

\[ G_{red}(s) = \frac{K}{(1+sT)}e^{-sL} \]

reduziert wird. Dieses Streckenmodell wird im Englischen als FOPDT (First order plus delay time) bezeichnet. Die Steigung der Wendetangente ist gleichermaßen mit

\[ R = \frac{a}{L} \qquad und \qquad R = \frac{K}{T} \]

beschrieben. Durch diese Beziehung können wir die Parameter \(K,L,T\) auf die Parameter \(a,L\) umrechnen, es gilt \(a=RL= KL/T\).

Die Modellreduktion soll hier nicht besprochen werden. Es sei auf die gängige Literatur verwiesen.

Geschlossener Regelkreis (Schwingversuch)

In der modernen Form ist sowohl ein empirisches Vorgehen als auch ein modellbasiertes Vorgehen möglich. Für dieses Vorgehen muss die Strecke durch einen P-Regler destabilisiert werden können. Anders ausgedrückt, die Amplitudenreserve (Gain margin) muss kleiner als unendlich sein (\(G_M < \infty\)).

Empirisches Vorgehen

Der offene Regelkreis \(L(s) = K_cG(s)\) ergibt sich aus einer Strecke \(G(s)\) und einem P-Regler \(K_c\). Der geschlossene Regelkreis \(T(s) = \frac{L(s)}{1+L(s)}\) wird mit einem konstanten Wert \(U_{const}\) beaufschlagt. Danach wird der P-Regler \(K_c\) kontinuierlich erhöht, bis der geschlossene Regelkreis grenzstabil wird. Nun schwingt der Regelkreis mit der kritischen Periode \(T_c\), bzw. mit der kritischen Frequenz \(\omega_c\).

Die PID Parameter können dann aus der Tabelle

Reglertyp \(K_p\) \(T_i\) \(T_d\)
\(P\) \(0.5K_c\) \(-\) \(-\)
\(PI\) \(0.4K_c\) \(0.8T_c\) \(-\)
\(PID\) \(0.6K_c\) \(0.5T_c\) \(0.12T_c\)

entnommen werden.

Modellbasiertes Vorgehen

Liegt ein Model der Strecke vor, so können wir die Phasen- und Amplitudenreserve mit der Methode \(G_M\), \(P_M\), \(\omega_{gc}\), \(\omega_{pc}\) = control.margin(\(G(s)\)) errechnen lassen. Die Amplitudenreserve ist aber genau jene Verstärkung \(K_c = G_M\), welche den Regelkreis in die Grenzstabilität treibt. Es gilt also:

\[ \begin{split} K_c &= G_M \\ \omega_c &= w_{gc} \\ T_c &= 2 \pi / \omega_c \end{split} \]

Wir haben also die kritische Verstärkung \(K_c\) und die kritische Periode \(T_c\) aus einem Model ermittelt.

CODE: Beispiel

Gegeben sei die Übertragungsfunktion

\[ G(s) = \frac{10}{(s+1)(s+2)(s+3)(s+4)}. \]

Gesucht ist nun ein guter PID Regler. Wir wollen dafür das Ziegler-Nichols Tuning basierend auf einen Schwingversuch benutzen.

import numpy as np
import control as ct
import matplotlib.pyplot as plt
plt.style.use('ggplot')
s = ct.tf('s')
G = ct.tf([10], [1,10,35,50,24])

gm, pm, wgc, wpc = ct.margin(G)
Kc = gm
wc = wgc
Tc = 2*np.pi/wc

print(Kc, "kritische Verstärkung")
print(wc, "kritische Frequenz")
print(Tc, "kritische Periode")
12.600000000000003 kritische Verstärkung
2.23606797749979 kritische Frequenz
2.8099258924162904 kritische Periode

Im Bode-Diagramm muss der offene Regelkreis \(K_c \cdot G\) die \(0\) dB bei \(-180^{°}\) durchschreiten. Anders ausgedrückt, die Amplitudenreserve von \(K_c \cdot G\) muss \(0\) dB sein.

_ = ct.bode(G, dB=True)
_ = ct.bode(Kc*G, margins=True ,dB=True)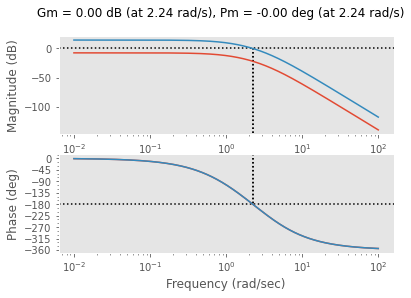

Im Nyquist-Diagramm muss der offene Regelkreis \(K_cG\) den Punkt \(-1\) durchschreiten.

plt.subplot(1,2,1)
_ = ct.nyquist(G)
plt.subplot(1,2,2)
_ = ct.nyquist([G,Kc*G])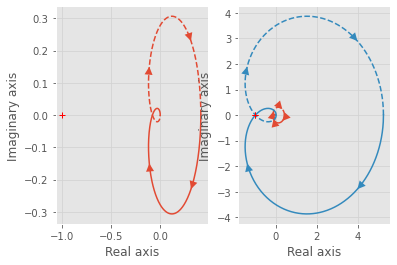

Zur Kontrolle können wir die Sprungantwort des geschlossenen Kreises \(\frac{Kc \cdot G}{1 + Kc \cdot G}\) analysieren. Wir sehen, dass der Regelkreis wie erwartet mit der kritischen Periode \(T_c\) schwingt.

L = Kc*G
T = ct.minreal(L/(1+L))
tout, yout = ct.step_response(T, 10)
plt.plot(tout, yout)
plt.title('Sprungantwort')
plt.show()
4 states have been removed from the model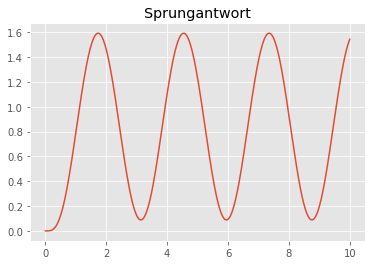

def create_pid(pid_type, Kp, Ti, Td, N):
    Gc = None
    H = None # controller in the backwardpass, here always 1
    
    if pid_type == 'P':
        Gc = Kp
        H = 1
    elif pid_type == 'PI':
        Gc = ct.tf([Kp*Ti,Kp*1],[Ti,0])
        H = 1
    elif pid_type == 'PID':
        num = [Kp*Ti*Td*(N+1)/N,Kp*(Ti+Td/N),Kp]
        den = [Ti*Td/N,Ti*1,0]
        Gc = ct.tf(num,den); 
        H = 1
        
    return Gc, H
def ziegler_nichols_table(pid_type, arg):
    Kp = None
    Ti = None
    Td = None
    N = None
    
    # frequency approach
    if len(arg) == 3:
        K = arg[0] 
        Tc = arg[1]
        N = arg[2]

        if pid_type == 'P':
            Kp = 0.5*K
        elif pid_type == 'PI':
            Kp=0.4*K
            Ti=0.8*Tc
        elif pid_type == 'PID':
            Kp=0.6*K 
            Ti=0.5*Tc 
            Td=0.12*Tc

    return Kp, Ti, Td, N
def ziegler_nichols(pid_type, arg):
    Kp, Ti, Td, N = ziegler_nichols_table(pid_type, arg)
    Gc, H = create_pid(pid_type, Kp, Ti, Td, N)
    return Gc, Kp, Ti, Td, H

Wir können wieder die drei Regler \(P, PI, PID\) vergleichen.

Die Regler ergeben sich dann zu

\[ G_P(s) = 6.3 \qquad G_{PI}(s) = 5.04 \left(1 + \frac{1}{2.2479} \right) \qquad G_{PID}(s) = 7.76 \left(1 + \frac{1}{1.405s} + 0.3372s\right). \]

[Gc1, Kp1, _, _, _] = ziegler_nichols('P',[Kc,Tc,10])
[Gc2, Kp2, Ti2, _, _] = ziegler_nichols('PI',[Kc,Tc,10])
[Gc3, Kp3, Ti3, Td3, _] = ziegler_nichols('PID',[Kc,Tc,10])

Tc1 = ct.feedback(G*Gc1,1)
Tc2 = ct.feedback(G*Gc2,1)
Tc3 = ct.feedback(G*Gc3,1)

plt.figure(figsize=(16,8))
tout, yout = ct.step_response(Tc1, 30)
plt.plot(tout, yout, label = 'P')
tout, yout = ct.step_response(Tc2, 30)
plt.plot(tout, yout, label = 'PI')
tout, yout = ct.step_response(Tc3, 30)
plt.plot(tout, yout, label = 'PID')
plt.legend()
plt.title('Sprungantwort ~ Ziegler-Nichols (Frequenzbereich)')
plt.show()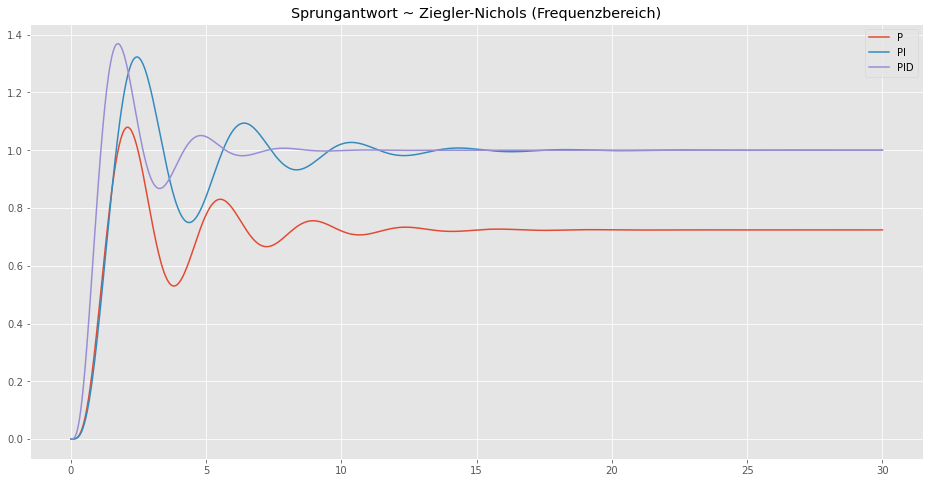

Der P-Regler besitzt eine bleibende Regelabweichung. Das Hinzufügen eines I-Anteils verhindert die bleibende Regelabweichung, führt aber oft zu zusätzlichen Schwingungen. Das Hinzufügen eines D-Anteils reduziert die Schwingungsneigung. Der PID hat die kleinste Anstiegszeit und die schnellste Ausregelzeit, jedoch ein etwas größeres Überschwingen.

Die Regler nach dem Ziegler-Nichols Tuning gelten generell als sehr aggressiv bzw. wenig robust. Deswegen werden bis heute immer wieder neue Faustformeln vorgeschlagen.

Fazit

Einstellregeln können sowohl an der Maschine als auch in der Simulation hilfreich sein, um die Parameter eines PID Reglers schnell in den richtigen Bereich zu bringen. Meist werden die Parameter aber per Hand fein eingestellt.

Zunehmend bieten industrielle Hersteller Tuning-Verfahren als Software- oder Hardwareprodukte an. Diese sind oft an die jeweilige Hardware angepasst.

Referenzen

  • Feedback Systems: An Introduction for Scientists and Engineers, Second Edition, 2020/2022 (Karl J. Aström, Richard M. Murray)
  • https://de.wikipedia.org/wiki/Geschichte_der_Regelungstechnik
  • PID control: the early years (Aidan O’Dwyer, 2005)
  • Optimum Settings for Automatic Controllers, (Ziegler Nichols, 1942)