import numpy as np
import scipy.signal as signal
import matplotlib.pyplot as plt
plt.style.use('ggplot')
import control as ctDas Ziel der MRAC Methode ist es, den Fehler \(e\) zwischen dem Referenzausgang \(y_r\) und dem Prozessausgang \(y_p\) gegen null zu bringen, \(e = y_r - y_p = 0\). Dies bedeutet jedoch nicht, dass die Reglerparameter zu den wahren Werten konvergieren. Die Konvergenz hängt besonders vom Referenz-Signal \(u_r\) ab. Diesen Aspekt wollen wir anhand von zwei einfachen Beispielen zeigen.
Beispiel 1: Direct MRAC, MIT Rule
Wir betrachten ein ganz einfaches Beispiel mit einem Steuerungsparameter \(\theta\), wie wir es in dem Blogeintrag
Adaptive Regelung - Direct MRAC, MIT Rule, Verstärkung
besprochen haben. Wir nehmen für \(G(s) = 1\) an, womit der Prozess mit \(y=bu\) beschrieben ist. Der Regler wird mit \(u_p = \theta u_r\) angegeben, der Referenz-Ausgang ist durch \(y_r = b_r u_r\) definiert. Der Fehler kann nun mit
\[ e = (b\theta - b_r)u_r = k(\theta - \theta^{\ast})u_c \]
angeben werden, wobei \(\theta^{\ast} = \frac{b_r}{b}\) gilt. Das MIT Gesetz liefert die folgende Differenzialgleichung für die Adaption:
\[ \dfrac{d\theta}{dt} = - \gamma k^2 u_c^2 \left( \theta - \theta^{\ast} \right) \]
Die Lösung dieser Gleichung lautet
\[ \theta(t) = \theta^{\ast} + \left( \theta_0 - \theta^{\ast} \right)e^{-\gamma k^{2} I_t} \]
wobei \(I_t\) durch das Integral
\[ I_t = \int_{0}^{t} u_c^2 (\tau) d\tau \]
definiert wird. Die Lösung für \(\theta(t)\) in den Fehler eingesetzt, ergibt die Gleichung
\[ e(t) = k u_c(t) \left( \theta_0 - \theta^{\ast} \right)e^{-\gamma k^2 I_t}. \]
Der Fehler geht also immer zu null, weil entweder das Integral \(I_t\) divergiert oder das Referenz-Signal verschwindet \(u_r(t) \rightarrow 0\). Die Entwicklung des Adaptionsparameters \(\theta(t)\) hängt also vom Eingangssignal ab.
Code
# linear system
b = 1
s = ct.tf('s')
G_plant_tf = b*s/s
# io model
io_plant = ct.LinearIOSystem(
G_plant_tf,
inputs=('up'),
outputs=('yp'),
states=0,
name='plant'
)# linear system
br = 2
G_model_tf = br*s/s
# io model
io_ref_model = ct.LinearIOSystem(
G_model_tf,
inputs=('ur'),
outputs=('yr'),
states=0,
name='ref_model'
)def adaptive_controller_state(t, x, u, params):
"""Internal state of adpative controller, f(t,x,u;p)"""
# parameters
gam = params["gam"] # adaptation gain, aka. learning rate
signb = params["signb"]
# controller inputs
ur = u[0]
yp = u[1]
yr = u[2]
# controller states
# theta = x[0] # is not needed here
# algebraic relationships
e = yr - yp
# dynamics xd = f(x,u)
d_theta = gam*yr*e*signb
return [d_theta]def adaptive_controller_output(t, x, u, params):
"""Algebraic output from adaptive controller, g(t,x,u;p)"""
# controller inputs
ur = u[0]
yp = u[1]
yr = u[2]
# controller state
theta = x[0]
# control law
up = theta*ur
return [up, theta]params={"gam":1,"signb":np.sign(b)}
io_controller = ct.NonlinearIOSystem(
adaptive_controller_state,
adaptive_controller_output,
inputs=3,
outputs=('up', 'theta'),
states=1,
params=params,
name='control',
dt=0
)io_closed = ct.InterconnectedSystem(
(io_plant, io_ref_model, io_controller),
connections=(
('plant.up', 'control.up'),
('control.u[1]', 'plant.yp'),
('control.u[2]', 'ref_model.yr')
),
inplist=('control.u[0]', 'ref_model.ur'),
outlist=('plant.yp', 'ref_model.yr', 'control.up', 'control.theta'),
dt=0
)# set initial conditions
X0 = np.zeros((1, 1))
X0[0] = 0 # state of system# set simulation duration and time steps
Tend = 6
dt = 0.1
# define simulation time span
t_vec = np.arange(0, Tend, dt)
# define control input
ur_vec = np.zeros((2, len(t_vec)))
ur_vec[0, :20] = 1
ur_vec[1, :] = ur_vec[0, :]# simulate the system, with different gammas
tout1, yout1 = ct.input_output_response(io_closed, t_vec, ur_vec, X0, params={"gam":0.5})
tout2, yout2 = ct.input_output_response(io_closed, t_vec, ur_vec, X0, params={"gam":1})
tout3, yout3 = ct.input_output_response(io_closed, t_vec, ur_vec, X0, params={"gam":2})plt.figure(figsize=(16,8))
plt.subplot(3,1,1)
plt.plot(tout2, yout1[0,:], label=r'$y_{\gamma = 0.5}$')
plt.plot(tout2, yout2[0,:], label=r'$y_{\gamma = 1.0}$')
plt.plot(tout3, yout3[0,:], label=r'$y_{\gamma = 2.0}$')
plt.plot(tout1, yout1[1,:] ,label=r'$y_{soll}$', linestyle="--")
plt.legend(fontsize=14)
plt.title('Systemantworten')
plt.subplot(3,1,2)
plt.plot(tout1, yout1[2,:], label=r'$\gamma = 0.5$')
plt.plot(tout2, yout2[2,:], label=r'$\gamma = 1.0$')
plt.plot(tout3, yout3[2,:], label=r'$\gamma = 2.0$')
plt.legend(loc=4, fontsize=14)
plt.title(r'Regler $u_p$')
plt.subplot(3,1,3)
plt.plot(tout1, yout1[1,:]-yout1[0,:], label=r'$\gamma = 0.5$')
plt.plot(tout2, yout2[1,:]-yout2[0,:], label=r'$\gamma = 1.0$')
plt.plot(tout3, yout3[1,:]-yout3[0,:], label=r'$\gamma = 2.0$')
plt.legend(loc=4, fontsize=14)
plt.title(r'Fehler $e$')
plt.show()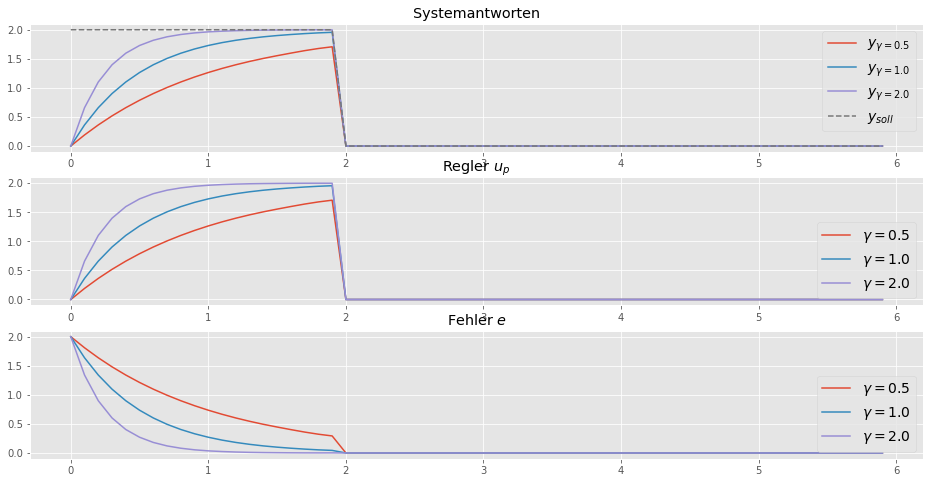
plt.figure(figsize=(16,8))
plt.plot(tout1, yout1[3,:], label=r'$\gamma = 0.5$')
plt.plot(tout2, yout2[3,:], label=r'$\gamma = 1.0$')
plt.plot(tout3, yout3[3,:], label=r'$\gamma = 2.0$')
plt.legend(loc=4, fontsize=14)
plt.title(r'Adaptionsparameter $\theta$')
plt.show()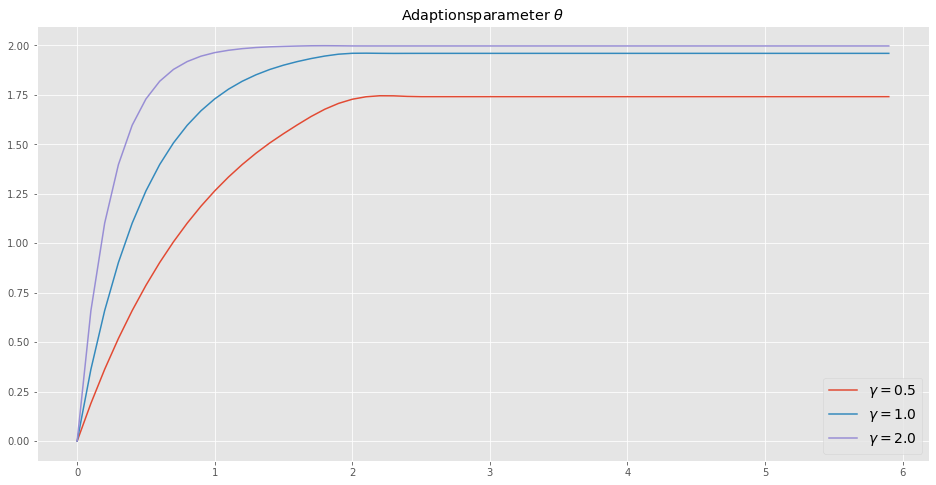
Wenn \(u_r = 0\) gilt, dann folgt \(e = 0\) und die Parameter werden nicht weiter angepasst. Weiters sehen wir den Einfluss von \(\gamma\).
Das ein Sprung als Referenz-Signal nicht immer eine ausreichende Anregung ist, wollen wir anhand eines weiteren Beispiels besprechen.
Beispiel 2: Direct MRAC, Lyapunov Rule
Aufgrund des Beispiels 1 könnte man meinen, dass es genügt \(u_r \neq 0\) zu wählen, damit die Adaptionsparameter zu den wahren Werten konvergieren. Dem ist aber nicht so. Selbst wenn also \(u_r \neq 0\) gilt, so werden womöglich die wahren Werte nicht erreicht. Das wollen anhand eines weiteren Beispiels besprechen.
Es sei ein System der Form
\[ \dot{x}_p(t) = a x_p(t) + b u_p(t) \]
gegeben, wobei \(u_p(t)\) der Eingang und \(x_p(t)\) ein messbarer Zustand ist. Die Modellparameter \(a\) und \(b\) sind unbekannt. Das geschlossene System soll nun wie das Modell
\[ \dot{x}_r(t) = a_r x_r(t) + b_r u_r(t) \]
verhalten. Das wollen wir mit dem Regler
\[ u_p(t) = k_x(t)x_p(t) + k_r(t)u_r(t) \]
erreichen, wobei \(k_x(t)\) ein Regelparameter (Feedback Gain) und \(k_r(t)\) ein Steuerungsparameter (Feedforward Gain) entspricht. Beide Parameter werden ständig angepasst und verändern sich dann natürlich über die Zeit.
Zur Anpassung der Parameter verwenden wir das Lyapunov-Gesetz:
\[ \begin{split} \dot{k}_x &= \gamma x_p e\\ \dot{k}_r &= \gamma u_r e \end{split} \]
Dabei ist der Fehler wieder duch \(e=x_r - x_p\) gebeben und \(\gamma\) ist eine Adaptionsverstärkung (Adaption Gain).
Die Herleitung des Lyapunov-Gesetzes (Lyapunov Rule) wird später nachgereicht. Hier wollen wir nur diese Methode implementieren und die Auswirkung der des Referenz-Signals \(u_r\) studieren.
Dazu wählen wir zwei verschiedene Referenz-Signale: - Sprung - Sinus
Code
# linear system
Ap = 1.
Bp = 3
Cp = 1
Dp = 0
G_plant_ss = ct.StateSpace(Ap,Bp,Cp,Dp)
# io_plant_model
io_plant = ct.LinearIOSystem(
G_plant_ss,
inputs=('up'),
outputs=('xp'),
states=('xp'),
name='plant'
)# linear system
Ar = -4
Br = 4
Cr = 1
Dr = 0
G_model_ss = ct.StateSpace(Ar,Br,Cr,Dr)
# io_ref_model
io_ref_model = ct.LinearIOSystem(
G_model_ss,
inputs=('ur'),
outputs=('xr'),
states=('xr'),
name='ref_model'
)kx_star = (Ar-Ap)/Bp
print(f"Der optimale Wert für {kx_star = }")
kr_star = (Br)/Bp
print(f"Der optimale Wert für {kr_star = }")Der optimale Wert für kx_star = -1.6666666666666667
Der optimale Wert für kr_star = 1.3333333333333333def adaptive_controller_state(t, x, u, params):
"""Internal state of adpative controller, f(t,x,u;p)"""
# parameters
gam = params["gam"]
# controller inputs
ur = u[0]
xp = u[1]
xr = u[2]
# controller states
x1 = x[0] # kx
x2 = x[1] # kr
# algebraic relationships
e = xr - xp
# dynamics xd = f(x,u)
d_x1 = gam*xp*e
d_x2 = gam*ur*e
return [d_x1, d_x2]def adaptive_controller_output(t, x, u, params):
"""Algebraic output from adaptive controller, g(t,x,u;p)"""
# controller inputs
ur = u[0]
xp = u[1]
xr = u[2]
# controller state
kx = x[0]
kr = x[1]
# control law
up = kx*xp + kr*ur
return [up, kx, kr]params={"gam":1, "Ar":Ar, "Br":Br}
io_controller = ct.NonlinearIOSystem(
adaptive_controller_state,
adaptive_controller_output,
inputs=3,
outputs=('up', 'kx', 'kr'),
states=2,
params=params,
name='control',
dt=0
)io_closed = ct.InterconnectedSystem(
(io_plant, io_ref_model, io_controller),
connections=(
('plant.up', 'control.up'),
('control.u[1]', 'plant.xp'),
('control.u[2]', 'ref_model.xr')
),
inplist=('control.u[0]', 'ref_model.ur'),
outlist=('plant.xp', 'ref_model.xr', 'control.up', 'control.kx', 'control.kr'),
dt=0
)# set initial conditions
X0 = np.zeros((4, 1))
X0[0] = 0 # state of plant
X0[1] = 0 # state of ref_model
X0[2] = 0 # state of controller
X0[3] = 0 # state of controllerSprung als Anregeung
Als Referenz-Signal \(u_r = \sigma(t)\) wird ein Sprung gewählt.
# set simulation duration and time steps
n_steps = 1000
Tend = 6
# define simulation time span
t_vec = np.linspace(0, Tend, n_steps)
# define control input
ur_vec = np.zeros((2, n_steps))
sin = np.sin(1. * np.pi * t_vec)
ur_vec[0, :] = 4
ur_vec[1, :] = ur_vec[0, :]# simulate the system, with different gammas
tout1, yout1 = ct.input_output_response(io_closed, t_vec, ur_vec, X0, params={"gam":2.0})plt.figure(figsize=(16,8))
plt.subplot(3,1,1)
plt.plot(tout1, yout1[0,:], label=r'$y_{\gamma = 2.0}$')
plt.plot(tout1, yout1[1,:] ,label=r'$y_{r}$')
plt.legend(loc=4)
plt.title('Systemantworten $y_p, (y_r)$')
plt.subplot(3,1,2)
plt.plot(tout1, yout1[2,:], label=r'$u$')
plt.legend(loc=4)
plt.title(r'Regler $u_p$')
plt.subplot(3,1,3)
plt.plot(tout1, yout1[0,:] - yout1[1,:], label=r'$e_{\gamma = 2.0}$')
plt.legend(loc=4)
plt.title('Fehler $e$')
plt.show()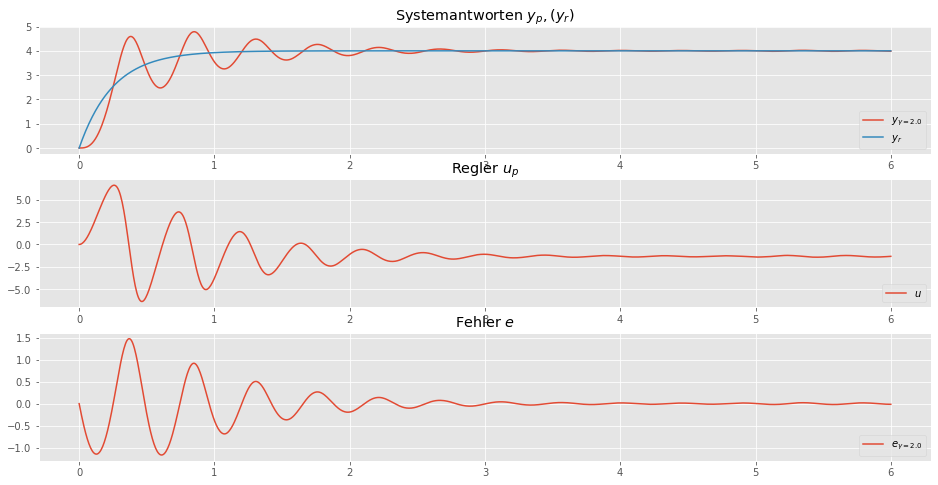
Der Fehler \(e = x_r - x_p \approx 0\) verschwindet.
plt.figure(figsize=(16,8))
plt.subplot(2,1,1)
plt.plot(tout1, yout1[3,:], label=r'$\gamma = 2.0$')
plt.hlines(kx_star,0,Tend,linestyle='--',label=r'$k_x^{\ast}$')
plt.legend(loc=4)
plt.title(r'Reglerparameter $k_x$')
plt.subplot(2,1,2)
plt.plot(tout1, yout1[4,:], label=r'$\gamma = 2.0$')
plt.hlines(kr_star,0,Tend,linestyle='--', label=r'$k_r^{\ast}$')
plt.legend(loc=4)
plt.title(r'Reglerparameter $k_r$')
plt.show()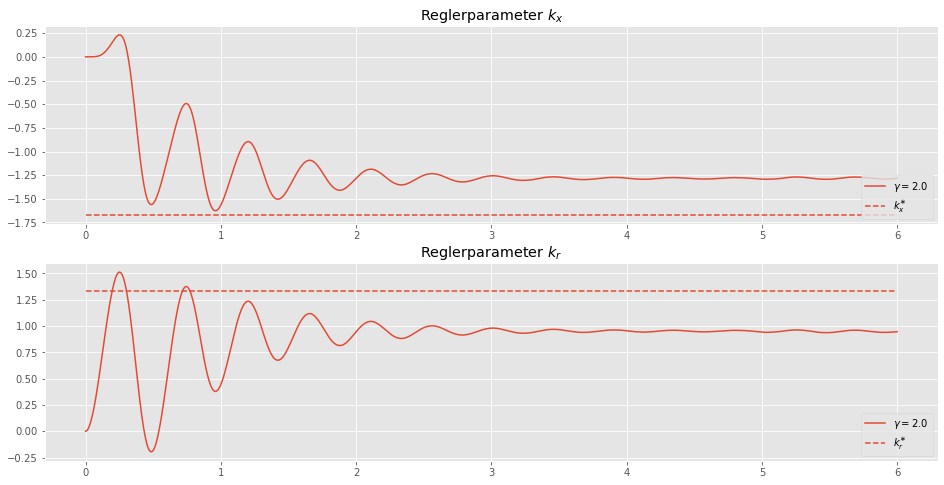
Die Adaptionsparameter des Regler konvergieren hier zwar, aber nicht zum wahren Wert, da ab eines gewissen Zeitpunkts, kein nennenswerter Fehler zur Verfügung steht. Das Referenz-Signal ist also nicht geeignet, um das System genügen anzuregen. Deshalb wollen wir ein anderes Signal als Referenz-Signal wählen.
Sinus als Anregeung
Als Referenz-Signal \(u_r = \sin(t)\) wird ein Sinus gewählt.
tout2, yout2 = ct.input_output_response(io_closed, t_vec, ur_vec*sin, X0, params={"gam":2.0})plt.figure(figsize=(16,8))
plt.subplot(3,1,1)
plt.plot(tout2, yout2[0,:], label=r'$y_{\gamma = 2.0}$')
plt.plot(tout2, yout2[1,:] ,label=r'$y_{r}$')
plt.legend(loc=4)
plt.title('Systemantworten $y_p, (y_r)$')
plt.subplot(3,1,2)
plt.plot(tout2, yout2[2,:], label=r'$u$')
plt.legend(loc=4)
plt.title(r'Regler $u_p$')
plt.subplot(3,1,3)
plt.plot(tout2, yout2[0,:] - yout2[1,:], label=r'$e_{\gamma = 2.0}$')
plt.legend(loc=4)
plt.title('Fehler $e$')
plt.show()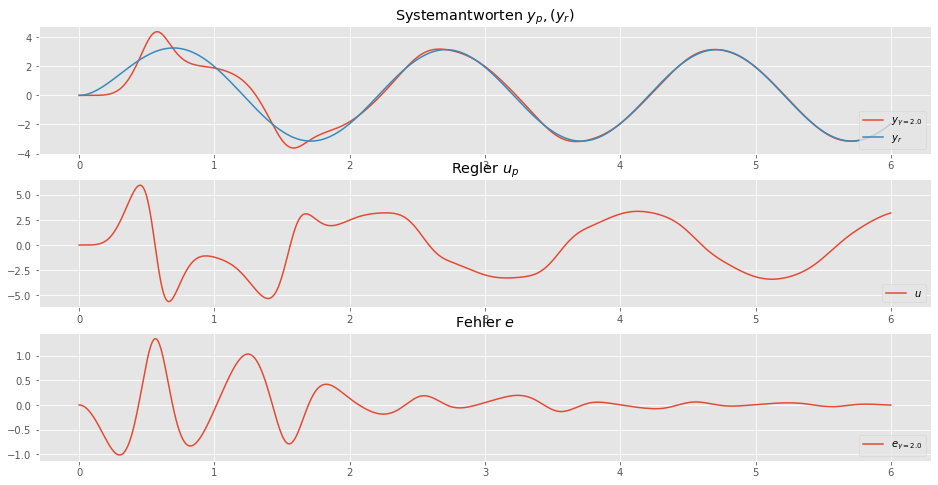
Auch hier veschwindet der Fehler \(e = y_r - y_p \approx 0\).
plt.figure(figsize=(16,8))
plt.subplot(2,1,1)
plt.plot(tout2, yout2[3,:], label=r'$\gamma = 2.0$')
plt.hlines(kx_star,0,Tend,linestyle='--',label=r'$k_x^{\ast}$')
plt.legend(loc=4)
plt.title(r'Reglerparameter $k_x$')
plt.subplot(2,1,2)
plt.plot(tout2, yout2[4,:], label=r'$\gamma = 2.0$')
plt.hlines(kr_star,0,Tend,linestyle='--',label=r'$k_r^{\ast}$')
plt.legend(loc=4)
plt.title(r'Reglerparameter $k_r$')
plt.show()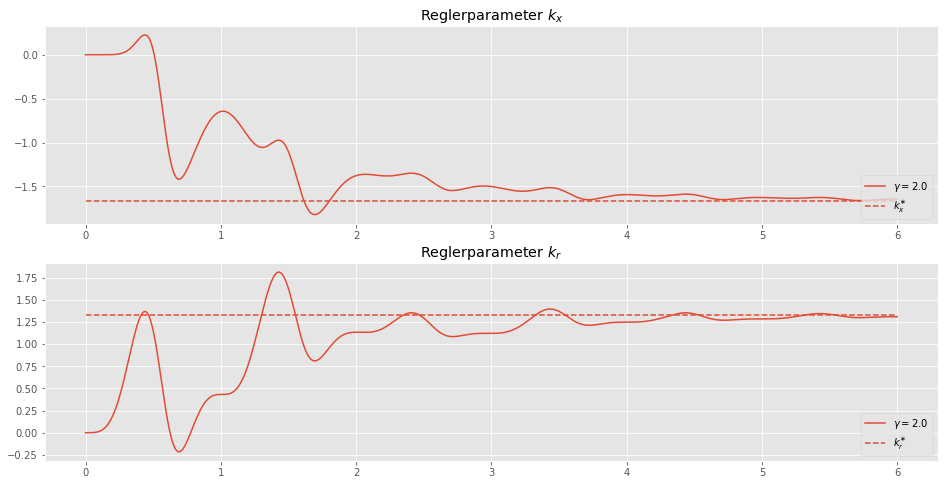
Wie wir sehen, konvergieren die Parameter zum wahren Wert. Der Sinus als Referenz-Signal ist also deutlich besser geeignet als der Sprung. Wir sehen weiters, dass das Verhalten vom Problem abhängig ist. Während der Sprung für das Problem im Beispiel 1 ausreichend ist, gilt das für das Beispiel 2 nicht.
Fazit
Die Konvergenz der Adaptionsparameter hängt von der Wahl des Referenz-Signals \(u_r\) ab. Dieser Sachverhalt wird in der Literatur auch unter dem Begriff Persistent Excitation Condition verhandelt. Das Referenz-Signal muss das System genügend anregen um Daten mit Informationsgehalt zu erzeugen, aus denen sich dann die Parameter bestimmen lassen.
Die Persistent Excitation Condition ist für die adaptive Regelung, die Systemidentifikation als auch das bestärkende Lernen von Bedeutung. Deswegen studieren wir diese in einem späteren Blogeintrag genauer. Zuvor wollen wir aber besser mit der adaptiven Regelung vertraut werden.
Das obige Verhalten hängt nicht nur von der Art des Signals \(u_r\) ab, sondern auch von der Amplitude \(|\gamma|\cdot|u_r|\). Normalisierte Algorithmen adressieren diesen Aspekt der adaptiven Regelung. Im nächsten Blogeintrag werden wir deshalb normalisierte Algorithmen besprechen.
Referenzen
- Adaptive Control, Second Editon, 2008 (Karl J. Aström, Björn Wittenmark)
- Model-Reference Adaptive Control: A primer, 2018 (Nhan T. Nguyen)
- Robust Adaptive control, 2012 (Petros A. Ioannou, Jing Sun)
- Deep Model Reference Adaptive Control 2019 (Girish Joshi, Girish Chowdhary)