import numpy as np
import scipy.signal as signal
import matplotlib.pyplot as plt
plt.style.use('ggplot')
import control as ctDie Adaptionsverstärkung (Adaption Gain) \(\gamma\) ist ein sogenannter Hyperparameter, welcher vorab eingestellt werden muss. In der Praxis wird dieser Parameter anhand von Simulationen bestimmt. Das Referenz-Signal hat jedoch erheblichen Einfluss auf das Adaptionsverhalten. Je nach Referenz-Signal muss dann die Adaptionsverstärkung angepasst werden.
Normalisierte Algorithmen sind deutlich unabhängiger bezüglich des Referenz-Signals. Als Erstes wollen wir den Zusammenhang anhand einfacher Beispiele verstehen.
Bestimmung der Adaptionsverstärkung
Gegeben sei der Prozess \(bG(s)\) wobei \(G(s)\) bekannt und \(b\) unbekannt ist. Dabei sei angenommen, dass \(G(s)\) stabil ist. Das Referenz-Model sei mit \(b_rG(s)\) gegeben. Die Adaptionsverstärkung \(\gamma\) muss also vom Benutzer bestimmt werden.
Die Gleichungen des obigen Problems lauten:
\[ \begin{split} y_p &= b G(p) u_p \\ y_r &= b_r G(p) u_r \\ u_p &= \theta u_r \\ e &= y_p - y_r \\ \dfrac{d\theta}{dt} &= - \gamma y_r e \end{split} \]
wobei \(u_r\) das Referenz-Signal, \(y_r\) der Referenz-Ausgang, \(y_p\) der Prozess-Ausgang, \(\theta\) der Adaptionsparameter, \(p = \dfrac{d}{dt}\) ist ein Differenzial-Operator.
Durch das Einsetzen der obigen Gleichungen und das Eliminieren \(u_p\) und \(y_p\) ergibt sich die Gleichung
\[ \dfrac{d \theta}{dt} + \gamma y_r G(p) \theta u_r = \gamma y_r^2. \]
Diese Gleichung beschreibt das zeitliche Verhalten des Parameters und wird als Parametergleichung bezeichnet. Es sei darauf hingewiesen, dass es sich bei \(u_r = u_r(t)\) und \(y_r = y_r(t)\) um zeitliche Funktionen handelt. Dadurch ist die Parametergleichung ein zeitvariantes System welches ein kompliziertes Verhalten aufweist und schwierig zu analysieren ist. Folglich wollen wir eine Näherung vornehmen.
Konstante Signale
Unter der Annahme eines konstanten Referenz-Eingangs \(u_r^{o} = const\) und nach dem Verschieden der Transienten ergibt sich der eingeschwungene Referenz-Ausgang \(y_r^{o} = const\). Die Parametergleichung
ist nun ein lineares zeitinvariantes System (LTI), d.h. es hat konstante Koeffizienten. Im Bildbereich lässt sich die Gleichung mit
\[ s + \gamma y_r^{o}u_r^{o} b G(s) = s + \mu G(s) = 0 \]
angeben. Nun ist offensichtlich, dass sich das Verhalten des Parameters durch
\[ \mu = \gamma y_r^{o}u_r^{o} b \]
bestimmen lässt.
Theoretisch lassen sich die obigen Zusammenhänge benutzen, um die Adaptionsverstärkung \(\gamma\) zu bestimmen. Gegeben sei das System \(G = \dfrac{1}{s+1}\) mit \(b = 1\) und \(b_r = 2\). Nun können wir die Gleichung
\[ s + \mu G(s) = 0 \]
mit
\[ s^2 + s + \mu = s^2 + s + \gamma y_r^{o} u_r^{o} k \]
angeben. Eine gute Wahl für \(\mu\) wäre \(\mu = \gamma y_r^{o} u_r^{o} b = 1\). Wenn wir für \(u_r^{o} = 1\) annehmen und die Transienten nicht berücksichtigen, dann ergibt sich für \(y_r^{o} u_r^{o} = 2\). Daraus folgt \(\gamma = 0.5\). Eine Simulation kann in dem früheren Blogeintrag betrachtet werden.
In der Praxis ist dieses Vorgehen jedoch nicht möglich, da der Parameter \(b\) unbekannt und somit die Bestimmung von \(\gamma\) nicht möglich ist.
Stabilität
Für Prozesse \(G(s)\) höherer Ordnung (\(n > 2\)) können Adaptionsprozesse auch instabil werden. Dies wollen wir zuerst theoretisch analysieren und dann mit eine Simulation bestätigen.
Gegeben sei die Übertragungsfunktion
\[ G(s) = \dfrac{1}{s^2 + a_1s + a_2}. \]
Nun können wir die Gleichung
\[ s + \mu G(s) = 0 \]
mit
\[ s^3 + a_1 s + a_2 s + \mu = 0 \]
angeben, wobei \(\mu = \gamma y_r^{o}u_r^{o}b\) gilt.
Für
\[ \gamma y_r^{o} u_r^{o} b < a_1 a_2 \]
liegen alle Pole in der linken Halbebene und Parameter Gleichung wäre stabil. Setzen wir für die Parameter \(b = a_1 = a_2 = 1\) und \(u_r^{o} = y_r^{o} = 1\) ein, so erhalten wir die Ungleichung
\[\gamma < 1 .\]
Für die oben gewählten Parameter führt also ein \(\gamma\) kleiner \(1\) zu einem stabilen Adaptionsprozess.
Mithilfe von python-control können wir die Regelung implementieren und testen. Das obige Beispiel soll hier nun implementiert werden. Das Problem sei gegeben durch:
- \(G(s) = \dfrac{1}{s^2+s+1}\) (bekannt)
- \(b = 1\) (unbekannt)
- \(b_r = 1\) (bekannt, da vorgegeben)
- \(\gamma = 0.1\) (Adaptions-Verstärkung)
- \(u_r = 0.1 rect(\pi t)\) (Referenz-Signal)
- \(u_r = 1.0 rect(\pi t)\) (Referenz-Signal)
- \(u_r = 3.5 rect(\pi t)\) (Referenz-Signal)
Für die verschiedenen Referenz-Signal können wir für \(\gamma = 0.1\) die Tabelle angeben:
| \(u_r^{o}\) | \(\gamma\) | \(\mu\) | \(\mu\) < \(a_1a_2\) |
|---|---|---|---|
| 0.1 | 0.1 | 0.001 | 0.001 < 1 (wahr, stabil) |
| 1.0 | 0.1 | 0.1 | 0.1 < 1 (wahr, stabil) |
| 3.5 | 0.1 | 1.25 | 1.25 < 1 (falsch, instabil) |
# linear system
b = 1
s = ct.tf('s')
G_plant_tf = b/(s**2+s+1)
# io model
io_plant = ct.LinearIOSystem(
G_plant_tf,
inputs=('up'),
outputs=('yp'),
states=2,
name='plant'
)# linear system
br = 1
G_model_tf = br/(s**2+s+1)
# io model
io_ref_model = ct.LinearIOSystem(
G_model_tf,
inputs=('ur'),
outputs=('yr'),
states=2,
name='ref_model'
)def adaptive_controller_state(t, x, u, params):
"""Internal state of adpative controller, f(t,x,u;p)"""
# parameters
gam = params["gam"] # adaptation gain, aka. learning rate
signb = params["signb"]
normalized = params["normalized"]
# controller inputs
ur = u[0]
yp = u[1]
yr = u[2]
# controller states
# theta = x[0] # is not needed here
# algebraic relationships
e = yr - yp
phi = - yr*signb
alpha = 1e-6
# dynamics xd = f(x,u)
if normalized == False:
d_theta = -gam*phi*e
else:
d_theta = -gam*phi*e/(alpha+phi*phi)
return [d_theta]def adaptive_controller_output(t, x, u, params):
"""Algebraic output from adaptive controller, g(t,x,u;p)"""
# controller inputs
ur = u[0]
yp = u[1]
yr = u[2]
# controller state
theta = x[0]
# control law
up = theta*ur
return [up, theta]params={"gam":1, "signb":np.sign(b), "normalized":False}
io_controller = ct.NonlinearIOSystem(
adaptive_controller_state,
adaptive_controller_output,
inputs=3,
outputs=('up', 'theta'),
states=1,
params=params,
name='control',
dt=0
)io_closed = ct.InterconnectedSystem(
(io_plant, io_ref_model, io_controller),
connections=(
('plant.up', 'control.up'),
('control.u[1]', 'plant.yp'),
('control.u[2]', 'ref_model.yr')
),
inplist=('control.u[0]', 'ref_model.ur'),
outlist=('plant.yp', 'ref_model.yr', 'control.up', 'control.theta'),
dt=0
)Nicht normalisierter Algorithmus
Als Erstes wollen wir nicht-normalisierte Algorithmen simulieren. Wir werden sehen, dass die oben gezeigten Instabilitäten auftreten. Wieder verwenden wir das MIT Gesetz
\[ \frac{d\theta}{dt} = - \gamma \frac{\partial J}{\partial \theta} = - \gamma e \frac{\partial e}{\partial \theta}. \]
Wir wollen jedoch eine etwas andere Notation einführen. Dazu führen wir
\[ \varphi = -\dfrac{\partial e}{\partial \theta} \]
für die negative Sensitivitätsableitung ein. Dann ergibt sich für das MIT Gesetz die Formulierung
\[ \dfrac{d\theta}{dt} = \gamma\varphi e. \]
# set initial conditions
X0 = np.zeros((5, 1))
X0[0] = 0 # state of system# set simulation duration and time steps
n_steps = 1000
Tend = 100
# define simulation time span
t_vec = np.linspace(0, Tend, n_steps)
# define control input
ur_vec = np.zeros((2, n_steps))
square = signal.square(2 * np.pi * 0.025 * t_vec)
ur_vec[0, :] = square
ur_vec[1, :] = ur_vec[0, :]# simulate the system, with different gammas
tout1_un, yout1_un = ct.input_output_response(io_closed, t_vec, ur_vec*0.1, X0, params={"gam":0.1})
tout2_un, yout2_un = ct.input_output_response(io_closed, t_vec, ur_vec*1.0, X0, params={"gam":0.1})
tout3_un, yout3_un = ct.input_output_response(io_closed, t_vec, ur_vec*3.5, X0, params={"gam":0.1})plt.figure(figsize=(16,8))
plt.subplot(3,1,1)
plt.plot(tout1_un, yout1_un[0,:], label=r'$u_r^{o}=0.1, \gamma = 0.1$')
plt.plot(tout1_un, yout1_un[1,:] ,label=r'$y_{soll}$', linestyle="--")
plt.legend(fontsize=14)
plt.title('$y$')
plt.subplot(3,1,2)
plt.plot(tout2_un, yout2_un[0,:], label=r'$u_r^{o}=1.0, \gamma = 0.1$')
plt.plot(tout2_un, yout2_un[1,:] ,label=r'$y_{soll}$', linestyle="--")
plt.legend(loc=4, fontsize=14)
plt.title('y')
plt.subplot(3,1,3)
plt.plot(tout3_un, yout3_un[0,:], label=r'$u_r^{o}=3.5, \gamma = 0.1$')
plt.plot(tout3_un, yout3_un[1,:] ,label=r'$y_{soll}$', linestyle="--")
plt.legend(loc=4, fontsize=14)
plt.title('y')
plt.show()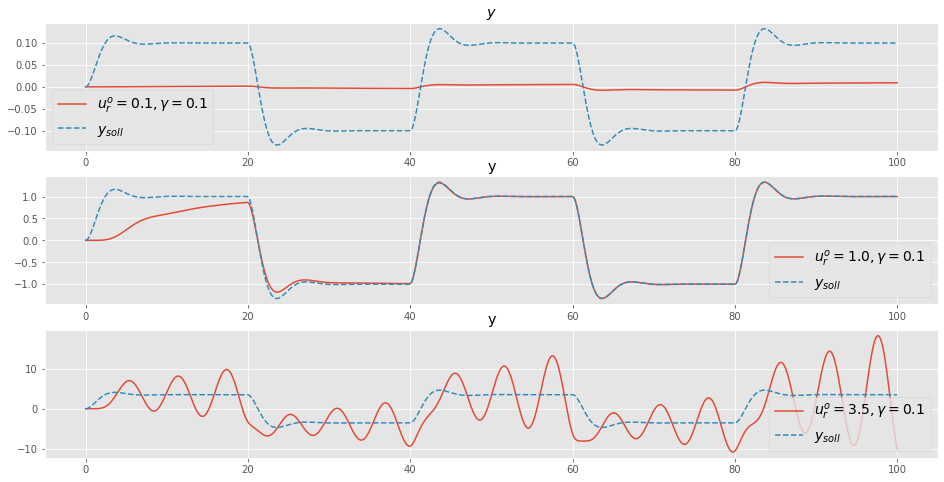
plt.figure(figsize=(16,8))
plt.plot(tout1_un, yout1_un[3,:], label=r'$u_r = 0.1$')
plt.plot(tout2_un, yout2_un[3,:], label=r'$u_r = 1.0$')
plt.plot(tout3_un, yout3_un[3,:], label=r'$u_r = 3.5$')
plt.legend(loc=4, fontsize=14)
plt.title(r'Adaptionsparameter $\theta$')
plt.show()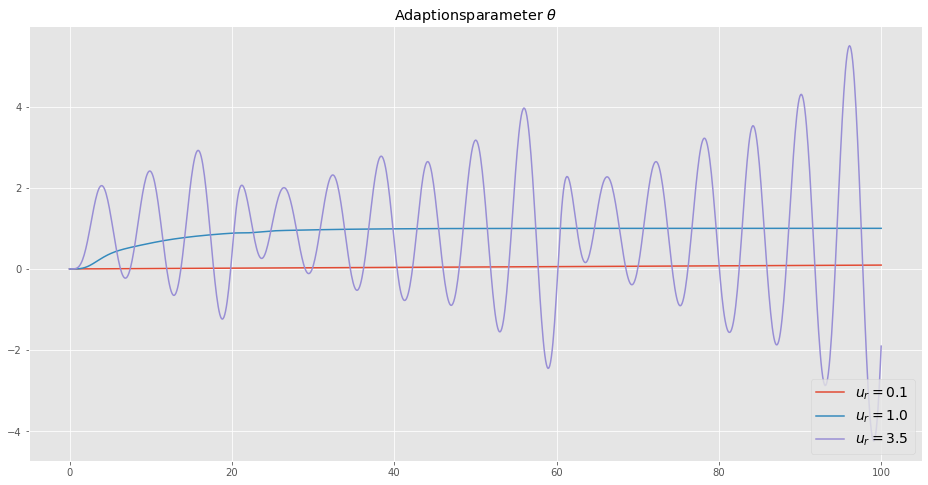
Wie wir sehen, ist das Verfahren für zu große Amplituden \(u_r = 3.5\) instabil, d.h. die Adaptionsverstärkung ist zu groß. Für zu kleine Amplituden \(u_r = 0.1\) ist die Adaptionsverstärkung zu klein. Das denkt sich mit den oben durchgeführten theoretische Überlegungen.
Anpassung der Adaptionsverstärkung
Eine Möglichkeit die oben gezeigten Schwierigkeiten zu begegnen, ist das Anpassen der Adaptionsverstärkung für den jeweiligen Fall:
| \(u_r^{o}\) | \(\gamma\) | \(\mu\) | \(\mu < a_1a_2\) |
|---|---|---|---|
| 0.1 | 10.0 | 0.1 | 0.1 < 1 (wahr, stabil) |
| 1.0 | 0.10 | 0.10 | 0.10 < 1 (wahr, stabil) |
| 3.5 | 0.10 | 0.125 | 0.125 < 1 (wahr, stabil) |
# simulate the system, with different gammas
tout1_un, yout1_un = ct.input_output_response(io_closed, t_vec, ur_vec*0.1, X0, params={"gam":10.0})
tout2_un, yout2_un = ct.input_output_response(io_closed, t_vec, ur_vec*1.0, X0, params={"gam":0.10})
tout3_un, yout3_un = ct.input_output_response(io_closed, t_vec, ur_vec*3.5, X0, params={"gam":0.01})plt.figure(figsize=(16,8))
plt.subplot(3,1,1)
plt.plot(tout1_un, yout1_un[0,:], label=r'$u_r^{o}=0.1, \gamma = 10.0}$')
plt.plot(tout1_un, yout1_un[1,:] ,label=r'$y_{soll}$', linestyle="--")
plt.legend(fontsize=14)
plt.title('y')
plt.subplot(3,1,2)
plt.plot(tout2_un, yout2_un[0,:], label=r'$u_r^{o}=1.0, \gamma = 0.1$')
plt.plot(tout2_un, yout2_un[1,:] ,label=r'$y_{soll}$', linestyle="--")
plt.legend(loc=4, fontsize=14)
plt.title('y')
plt.subplot(3,1,3)
plt.plot(tout3_un, yout3_un[0,:], label=r'$u_r^{o}=3.5, \gamma = 0.01$')
plt.plot(tout3_un, yout3_un[1,:] ,label=r'$y_{soll}$', linestyle="--")
plt.legend(loc=4, fontsize=14)
plt.title('y')
plt.show()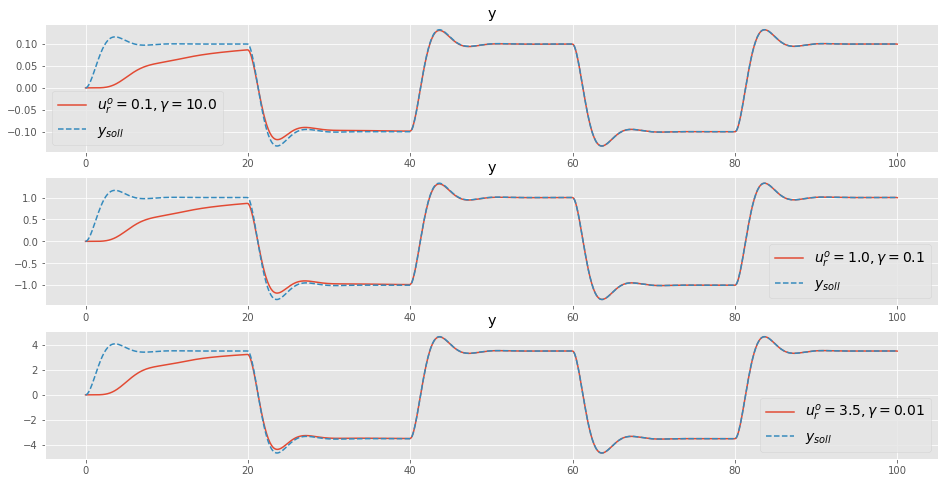
Dieses Vorgehen führt zu einem guten Adaptionsverhalten. Das jeweilige Anpassen der Adaptionsverstärkung bei veränderten Referenz-Signal \(u_r\) scheint jedoch nicht wirklich attraktiv. Die übliche Methode, um diesen Umstand abzuschwächen, ist der Einsatz von sogenannten normalisierten Algorithmen.
Normalisierter Algorithmus
Das MIT Gesetz lautet
\[ \dfrac{d\theta}{dt} = \gamma\varphi e \]
wobei wir \(\varphi = -\dfrac{\partial e}{\partial \theta}\) eingeführt haben.
Für den normalisierten Algorithmus wird das Adaptionsgesetz abgeändert
\[ \dfrac{d\theta}{dt} = \dfrac{\gamma \varphi e}{\alpha + \varphi^T\varphi} \]
wobei der Parameter \(\alpha > 0\) eingeführt wurde, um Probleme mit kleinen \(\varphi\) zu vermeiden.
Diese Adaptionsgesetz können wir wieder wie oben analysieren und wir erhalten
\[ s + \gamma \dfrac{\varphi^{o} u_r^{o}}{\alpha + {\varphi^{o}}^T\varphi^{o}} b G(s) = 0. \]
Da \(\varphi^{o}\) proportional zu \(u_r^{o}\) ist, verändern sich die Pole bezüglich der Signal-Level kaum.
Um die Effektivität dieser Vorgehensweise zu zeigen wollen wir die diesen normalisierten Algorithmus für $0.1 u_r, 1.0 u_r, 3.5 u_r $ verwenden, wobei immer die Adaptionsverstärkung \(\gamma = 0.1\) gewählt wird.
# simulate the system, with different gammas
tout1, yout1 = ct.input_output_response(io_closed, t_vec, ur_vec*0.1, X0, params={"gam":0.1, "normalized":True})
tout2, yout2 = ct.input_output_response(io_closed, t_vec, ur_vec*1.0, X0, params={"gam":0.1, "normalized":True})
tout3, yout3 = ct.input_output_response(io_closed, t_vec, ur_vec*3.5, X0, params={"gam":0.1, "normalized":True})plt.figure(figsize=(16,8))
plt.subplot(3,1,1)
plt.plot(tout2, yout1[0,:], label=r'$u_r^{o}=0.1, \gamma = 0.1}$')
plt.plot(tout1, yout1[1,:] ,label=r'$y_{soll}$', linestyle="--")
plt.legend(fontsize=14)
plt.title('y')
plt.subplot(3,1,2)
plt.plot(tout2, yout2[0,:], label=r'$u_r^{o}=1.0, \gamma = 0.1$')
plt.plot(tout1, yout2[1,:] ,label=r'$y_{soll}$', linestyle="--")
plt.legend(loc=4, fontsize=14)
plt.title('y')
plt.subplot(3,1,3)
plt.plot(tout3, yout3[0,:], label=r'$u_r^{o}=3.5, \gamma = 0.1$')
plt.plot(tout3, yout3[1,:] ,label=r'$y_{soll}$', linestyle="--")
plt.legend(loc=4, fontsize=14)
plt.title('y')
plt.show()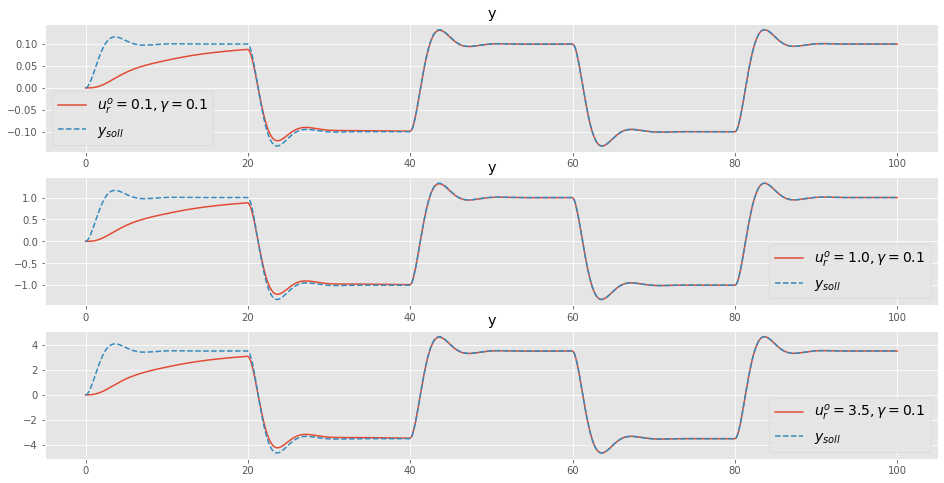
plt.figure(figsize=(16,8))
plt.plot(tout1, yout1[3,:], label=r'$u_r^{o} = 0.1$')
plt.plot(tout2, yout2[3,:], label=r'$u_r^{o} = 1.0$')
plt.plot(tout3, yout3[3,:], label=r'$u_r^{o} = 3.5$')
plt.legend(loc=4, fontsize=14)
plt.title(r'Adaptionsparameter $\theta$')
plt.show()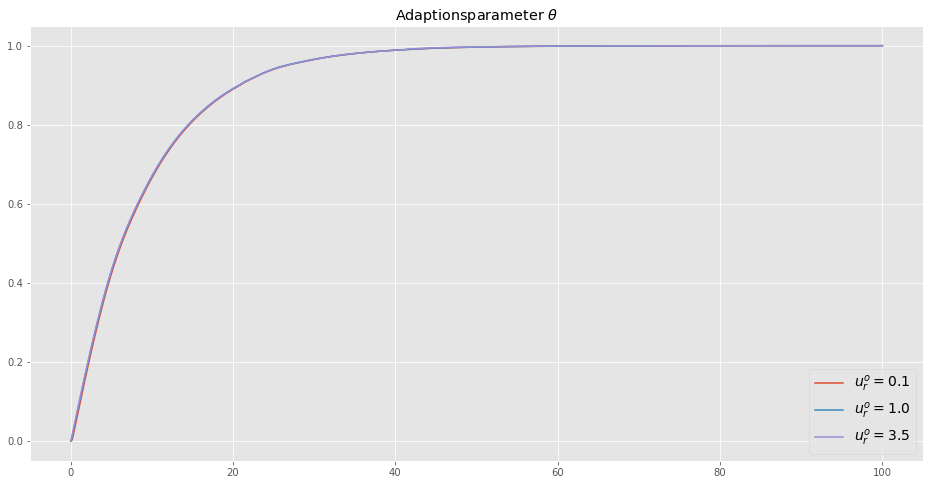
Die Entwicklung des Adaptionsparameters \(\theta\) wird kaum vom Referenz-Signal beeinflusst.
Fazit
Normalisierte Algorithmen sind innerhalb der MRAC Methoden oft anzutreffen. Diese reduzieren die Abhängigkeit bezüglich der Signal-Level des Referenz-Signals. Somit können die Adaptionsverstärkungen unabhängig dieser Signal-Level gewählt werden.
Normalisierte Algorithmen werden auch im Zusammenhang der Fast Adaptation besprochen. Oft ist es notwendig, das der Folgefehler schnell reduziert wird. Dazu werden große Adaptionsverstärkungen benötigt, welche aber leicht zu Instabilitäten führen können. Normalisierte Algorithmen können auch hier Abhilfe schaffen.
Lyapunove Rule
Beinahe alle bisher besprochenen Aspekte basierten auf dem Einsatz des MIT Gesetzes (MIT Rule). Wahrscheinlich ist das MIT Gesetz das meist eingesetzte Verfahren der adaptive Regelung. Jedoch dominieren in der neueren Literatur, Methoden basierend auf der Lyapunov Theorie. Deshalb werden wir uns in den nächsten Blogeinträgen intensiv mit der Lyapunov Theorie beschäftigen und später zu MRAC zurückkehren.
Referenzen
- Adaptive Control, Second Editon, 2008 (Karl J. Aström, Björn Wittenmark)
- Model-Reference Adaptive Control: A primer, 2018 (Nhan T. Nguyen)
- Robust Adaptive control, 2012 (Petros A. Ioannou, Jing Sun)
- Deep Model Reference Adaptive Control 2019 (Girish Joshi, Girish Chowdhary)