import numpy as np
import scipy.signal as signal
import matplotlib.pyplot as plt
plt.style.use('ggplot')
import control as ctIm letzten Blogeintrag haben wir ein minimales MRAC Problem besprochen und in Python implementiert. Hier wollen wir nun dieselbe Methode für ein System 1. Ordnung besprechen.
Model-Reference Adpative Control (MRAC)
Systeme 1.Ordnung
Oft können physikalische Prozesse mit Differenzialgleichungen höhere Ordnung beschrieben werden, und liegen in der Form
\[ \begin{split} & y^{(n)}(t)a_n + y^{(n-1)}(t)a_{n-1} + \cdots + \dot{y}(t)a_1 + y(t)a_{0} \\ & \quad = u^{(n)}(t)b_n + u^{(n-1)}(t)b_{n-1} + \cdots + \dot{u}(t)b_1 + u(t)b_{0} \end{split} \]
in Textbüchern vor. Diese können immer auf Systeme 1. Ordnung
\[ \begin{split} \dot{x} &= A_cx + b_cu \\ y &= c_c^Tx + d_cu \end{split} \rightarrow \begin{cases} \frac{d}{dt} \underset{\dot{\tilde{x}}}{\underbrace{ \begin{bmatrix} \tilde{x}_1 \\ \tilde{x}_2 \\ \vdots \\ \tilde{x}_{n-1} \\ \tilde{x}_n \end{bmatrix}}} = \underset{A_c = T^{-1}AT}{\underbrace{ \begin{bmatrix} 0 & 1 & \dots & 0 \\ 0 & 0 & \dots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \dots & 1 \\ -a_0 & -a_1 & \dots & -a_{n-1} \end{bmatrix}}} \underset{\tilde{x}}{\underbrace{ \begin{bmatrix} \tilde{x}_1 \\ \tilde{x}_2 \\ \vdots \\ \tilde{x}_{n-1} \\ \tilde{x}_n \end{bmatrix}}} + \underset{b_c = T^{-1}b}{\underbrace{\begin{bmatrix} 0 \\ 0 \\ \vdots \\ 0 \\ 1 \end{bmatrix}}}u, \\ y = \underset{c_c^T=c^TT}{\underbrace{\begin{bmatrix} \tilde{c}_0 & \tilde{c}_1 & \dots & \tilde{c}_{n-1} \end{bmatrix}}} \underset{\tilde{x}}{\underbrace{ \begin{bmatrix} \tilde{x}_1 \\ \tilde{x}_2 \\ \vdots \\ \tilde{x}_{n-1} \\ \tilde{x}_n \end{bmatrix}}} + \underset{d_c}{\underbrace{d}} u \end{cases} \]
überführt werden. Siehe dazu den Blogeintrag, Repräsentation linearer Systeme.
Mit \(n\) wollen wir nun die Dimension des Zustandsvektors bezeichnen.
Direct MRAC: System 1.Ordnung mit \(n=1\)
Es sei ein System der Form
\[ \dot{x}_p(t) = a x_p(t) + b u_p(t) \]
gegeben, wobei \(u_p(t)\) der Eingang und \(x_p(t)\) ein messbarer Zustand ist. Die Modellparameter \(a\) und \(b\) sind unbekannt. Das geschlossene System soll sich nun wie das Modell
\[ \dot{x}_r(t) = a_r x_r(t) + b_r u_r(t) \]
verhalten. Das wollen wir mit dem Regler
\[ u_p(t) = k_x(t)x_p(t) + k_r(t)u_r(t) \]
erreichen, wobei \(k_x(t)\) ein Regelparameter (Feedback Gain) und \(k_r(t)\) ein Steuerungsparameter (Feedforward Gain) ist. Beide Parameter werden ständig angepasst und verändern sich dann natürlich über die Zeit. Für eine übersichtliche Notation wollen wir aber die zeitliche Abhängigkeit ab hier nicht extra darstellen.
Wenn wir für die Reglerparameter die Werte
\[ \begin{split} k_x &= k_x^{*} = \frac{a_r-a}{b} \\ k_r &= k_r^{*} = \frac{b_r}{b} \end{split} \]
wählen würden, so hätten beide Systeme dasselbe Eingangs-Ausgangsverhalten. Da aber die Prozessparameter (\(a, b\)) unbekannt sind, ist dieses Vorgehen nicht möglich.
Um das MIT Gesetz (MIT Rule) anwenden zu können, führen wir den Fehler
\[ e = x_r - x_p \]
ein, wobei \(x_p\) der Ausgang des geschlossenen Kreises darstellt. Setzen wir den Regler in das System ein
\[ \dot{x}_p = a x_p + b u_p = a x_p + b k_x x_p + b k_r u_r = (a + b k_x) x_p + b k_r u_r, \]
so erhalten wir die Gleichung
\[ x_p = \frac{b k_r}{p - (a + b k_x)} u_r \]
mit dem Differentialoperator \(p = \frac{d}{dt}\).
Die Sensitivitätsableitungen \(\dfrac{de}{d\theta}\) ergeben sich zu:
\[ \begin{split} \frac{d e}{d k_r} &= - \frac{b}{p - (a + bk_x)}u_r \\ \frac{d e}{d k_x} &= - \frac{b^2k_r}{(p - (a + bk_x))^2}u_r = - \frac{b}{p - (a + bk_x)}x_p \end{split} \]
Diese Gleichungen sind auf die Parameter \(a\) und \(b\) angewiesen, welche aber unbekannt sind. Näherungsformeln sind also notwendig. Eine Möglichkeit ergibt sich, wenn die “perfekten” Werte für \(k_x=k_x^{*}\) und \(k_r=k_r^{*}\) eingesetzt werden, womit \(p-(a+bk_x^{*}) = p - a_r\) gilt. Wir können also die Näherung
\[ p - (a + bk_x) \approx p - a_r \]
nutzen, welche in der Nähe der “perfekten” Werte in jedem Fall Sinn ergibt. Diese Näherung eingesetzt und wir erhalten die Adaptionsgesetze
\[ \begin{split} \dot{k}_r &= - \gamma^{\prime} \left( - \frac{b}{p - a_r} u_r \right) e = - \gamma \left( \frac{a_r}{p - a_r} u_r \right) e \cdot \text{sign}(b) \\ \dot{k}_x &= - \gamma^{\prime} \left( - \frac{b}{p - a_r} x_p \right) e = - \gamma \left( \frac{a_r}{p - a_r} x_p \right) e \cdot \text{sign}(b) \end{split} \]
Um auch den Systemparameter \(b\) zu ersetzen, wurde hier eine neue Adaptionsverstärkung \(\gamma = - \gamma^{\prime} b/a_r\) eingeführt. Dadurch wurde auch der Filter normalisiert. Um auch das korrekte Vorzeichen für \(\gamma\) einzuführen, muss das Vorzeichen von \(b\) bekannt sein.
Wir können die Strecke
\[ G_p(s) = \frac{b}{s - a} \]
als auch das Referenz-Modell
\[ G_r(s) = \frac{b_r}{s - a_r} \]
als Übertragungsfunktion darstellen.
Auch die Adaptionsgesetze können im Frequenzbereich
\[ \begin{split} K_r(s) &= - \frac{\gamma}{s} \frac{a_r}{s - a_r} U_r(s) E(s) \cdot \text{sign}(b) \\ K_x(s) &= - \frac{\gamma}{s} \frac{a_r}{s - a_r} X_p(s) E(s) \cdot \text{sign}(b) \end{split} \]
angeschrieben werden. Diese Darstellung kann hilfreich sein, wenn Blockdiagramm-Umgebungen wie Matlab/Simulink zur Verfügung stehen. In Python existieren solche Umgebungen nur in einem sehr eingeschränkten Umfang. Auch ist der Zeitbereich die allgemeinere Darstellung und kann leicht auf den nichtlinearen Fall ausgeweitet und mit Maschine-Learning Ansätzen erweitert werden.
Um die Adaptionsgesetze implementieren zu können, benötigen wir eine Zustandsraumdarstellung. Dazu führen wir für \(\dfrac{a_r}{p-a_r}u_r\) und \(\dfrac{a_r}{p-a_r}x_p\) Zustandsgleichungen ein
\[ \begin{split} (p - a_r)x_1 &= a_r u_r \\ (p - a_r)x_3 &= a_r x_p \end{split} \]
und wenden den Operator \(p\) an (\(px_1 = \dot{x}_1\) und \(px_3 = \dot{x}_3\)). Somit erhalten wir ein Gleichungssystem 1. Ordnung
\[ \begin{split} \dot{x}_1 &= + a_r x_1 + a_r u_r \\ \dot{x}_3 &= + a_r x_3 + a_r x_p \end{split} \]
Durch das Einsetzen in die ursprünglichen Gleichungen erhalten wir das gesamte Gleichungssystem
\[ \begin{split} \dot{x}_1 &= + a_r x_1 + a_r u_r \\ \dot{x}_2 &= -\gamma x_1 \cdot e \cdot \text{sign}(b) \\ \dot{x}_3 &= + a_r x_3 + a_r x_p \\ \dot{x}_4 &= -\gamma x_3 \cdot e \cdot \text{sign}(b) \end{split} \]
des adaptiven Reglers.
Die Gleichung
\[ u_p = x_4 x_p + x_2 u_r \qquad (\rightarrow u_p = k_x x_p + k_r u_r) \]
beschreibt den Regler in den neuen Zuständen.
Beispiel
Mithilfe von python-control können wir die Regelung implementieren und testen.
Das obige Beispiel soll hier nun implementiert werden. Das Problem sei gegeben durch:
- \(a = 1\), \(b = 0.5\) (unbekannt)
- \(a_r = 2\), \(b_r = 2\) (bekannt, da vorgegeben)
- \(\gamma = 0.2, 1.0 ,5.\) (Adaptions-Verstärkung)
- \(u_r = square(2 \pi 0.05 t)\) (Referenz-Signal)
Die Strecke ist ein lineares System für welches wir die Klasse control.LinearIOSystem nutzen können.
# linear system
Ap = -1.
Bp = 0.5
Cp = 1
Dp = 0
G_plant_ss = ct.StateSpace(Ap,Bp,Cp,Dp)
# io_plant_model
io_plant = ct.LinearIOSystem(
G_plant_ss,
inputs=('up'),
outputs=('xp'),
states=('xp'),
name='plant'
)Das Referenz-Modell ist ein lineares System für welches wir die Klasse control.LinearIOSystem nutzen können.
# linear system
Ar = -2
Br = 2
Cr = 1
Dr = 0
G_model_ss = ct.StateSpace(Ar,Br,Cr,Dr)
# io_ref_model
io_ref_model = ct.LinearIOSystem(
G_model_ss,
inputs=('ur'),
outputs=('xr'),
states=('xr'),
name='ref_model'
)kr_star = (Br)/Bp
print(f"Der optimale Wert für {kr_star = }")
kx_star = (Ar-Ap)/Bp
print(f"Der optimale Wert für {kx_star = }")Der optimale Wert für kr_star = 4.0
Der optimale Wert für kx_star = -2.0Weil viele Adaptionsgesetze nichtlineare Funktionen sind, wollen wir die Klasse control.NonlinearIOSystem benutzen.
Diese Klasse erlaubt eine Implementation eines nichtlineares Systems der Form
\[ \begin{split} \dot{x} &= f(t, x, u; p) \\ y &= g(t, x, u; p) \\ \end{split}. \]
Dafür werden zwei Funktionen für \(f(t,x,u;p)\) und \(g(t,x,u;p)\) benötigt, welche der Klasse übergeben werden.
def adaptive_controller_state(t, x, u, params):
"""Internal state of adpative controller, f(t,x,u;p)"""
# parameters
gam = params["gam"]
Ar = params["Ar"]
Br = params["Br"]
signb = params["signb"]
# controller inputs
ur = u[0]
xp = u[1]
xr = u[2]
# controller states
x1 = x[0] #
x2 = x[1] # kr
x3 = x[2] #
x4 = x[3] # kx
# algebraic relationships
e = (xr - xp)
d_x1 = Ar*x1 + Ar*ur
d_x2 = - gam*(x1)*e*signb
d_x3 = Ar*x3 + Ar*xp
d_x4 = - gam*(x3)*e*signb
return [d_x1, d_x2, d_x3, d_x4]def adaptive_controller_output(_t, x, u, params):
"""Algebraic output from adaptive controller, g(t,x,u;p)"""
# controller inputs
ur = u[0]
xp = u[1]
xr = u[2]
# controller state
kr = x[1]
kx = x[3]
# control law
up = + kx*xp + kr*ur
return [up, kx, kr]params={"gam":1, "Ar":Ar, "Br":Br, "signb":np.sign(Bp)}
io_controller = ct.NonlinearIOSystem(
adaptive_controller_state,
adaptive_controller_output,
inputs=3,
outputs=('up', 'kx', 'kr'),
states=4,
params=params,
name='control',
dt=0
)Die drei Blöcke können mit control.InterconnectedSystem verschaltet werden.
io_closed = ct.InterconnectedSystem(
(io_plant, io_ref_model, io_controller),
connections=(
('plant.up', 'control.up'),
('control.u[1]', 'plant.xp'),
('control.u[2]', 'ref_model.xr')
),
inplist=('control.u[0]', 'ref_model.ur'),
outlist=('plant.xp', 'ref_model.xr', 'control.up', 'control.kx', 'control.kr'),
dt=0
)# set initial conditions
X0 = np.zeros((6, 1))
X0[0] = 0 # state of plant
X0[1] = 0 # state of ref_model
X0[2] = 0 # state of controller
X0[3] = 0 # state of controller
X0[4] = 0 # state of controller
X0[5] = 0 # state of controller# set simulation duration and time steps
Tend = 100
dt = 0.1
# define simulation time span
t_vec = np.arange(0, Tend, dt)
# define control input
uc_vec = np.zeros((2, len(t_vec)))
square = signal.square(2 * np.pi * 0.05 * t_vec)
uc_vec[0, :] = square
uc_vec[1, :] = uc_vec[0, :]plt.figure(figsize=(16,8))
plt.plot(t_vec, uc_vec[0,:])
plt.title(r'Anregungssignal $u_r$')
plt.show()
# simulate the system, with different gammas
tout1, yout1 = ct.input_output_response(io_closed, t_vec, uc_vec, X0, params={"gam":0.2})
tout2, yout2 = ct.input_output_response(io_closed, t_vec, uc_vec, X0, params={"gam":1.0})
tout3, yout3 = ct.input_output_response(io_closed, t_vec, uc_vec, X0, params={"gam":5.0})plt.figure(figsize=(16,8))
plt.subplot(2,1,1)
plt.plot(tout1, yout1[0,:], label=r'$y_{\gamma = 0.2}$')
plt.plot(tout2, yout2[0,:], label=r'$y_{\gamma = 1.0}$')
plt.plot(tout2, yout3[0,:], label=r'$y_{\gamma = 5.0}$')
plt.plot(tout1, yout1[1,:] ,label=r'$y_{r}$')
plt.legend(fontsize=14)
plt.title('Systemantworten $y_p, (y_r)$')
plt.subplot(2,1,2)
plt.plot(tout1, yout1[2,:], label=r'$u$')
plt.plot(tout2, yout2[2,:], label=r'$u$')
plt.plot(tout3, yout3[2,:], label=r'$u$')
plt.legend(loc=4, fontsize=14)
plt.title(r'Regler $u_p$')
plt.show()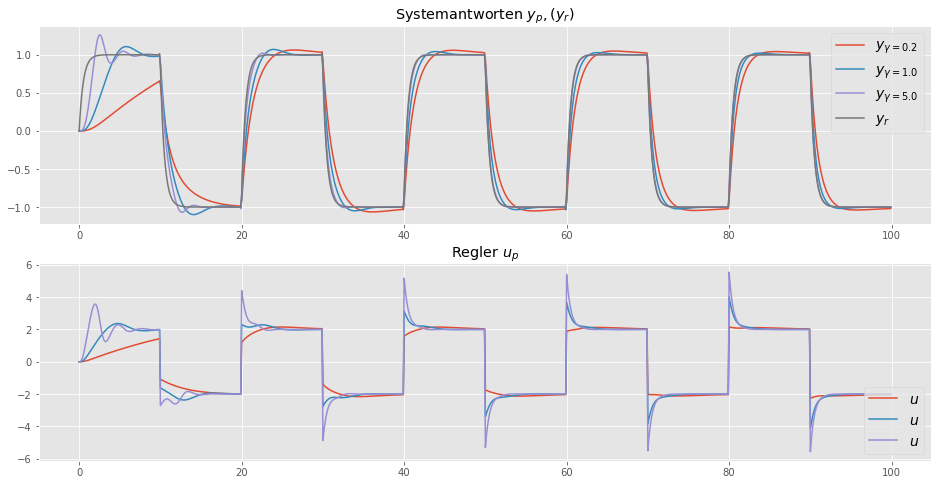
plt.figure(figsize=(16,8))
plt.subplot(2,1,1)
plt.plot(tout1, yout1[3,:], label=r'$\gamma = 0.2$')
plt.plot(tout2, yout2[3,:], label=r'$\gamma = 1.0$')
plt.plot(tout3, yout3[3,:], label=r'$\gamma = 5.0$')
plt.hlines(kx_star, 0, Tend, label=r'$k_x^{\ast}$', color='black', linestyle='--')
plt.legend(loc=4, fontsize=14)
plt.title(r'Reglerparameter $k_x$')
plt.subplot(2,1,2)
plt.plot(tout1, yout1[4,:], label=r'$\gamma = 0.2$')
plt.plot(tout2, yout2[4,:], label=r'$\gamma = 1.0$')
plt.plot(tout3, yout3[4,:], label=r'$\gamma = 5.0$')
plt.hlines(kr_star, 0, Tend, label=r'$k_r^{\ast}$', color='black', linestyle='--')
plt.legend(loc=4, fontsize=14)
plt.title(r'Reglerparameter $k_r$')
plt.show()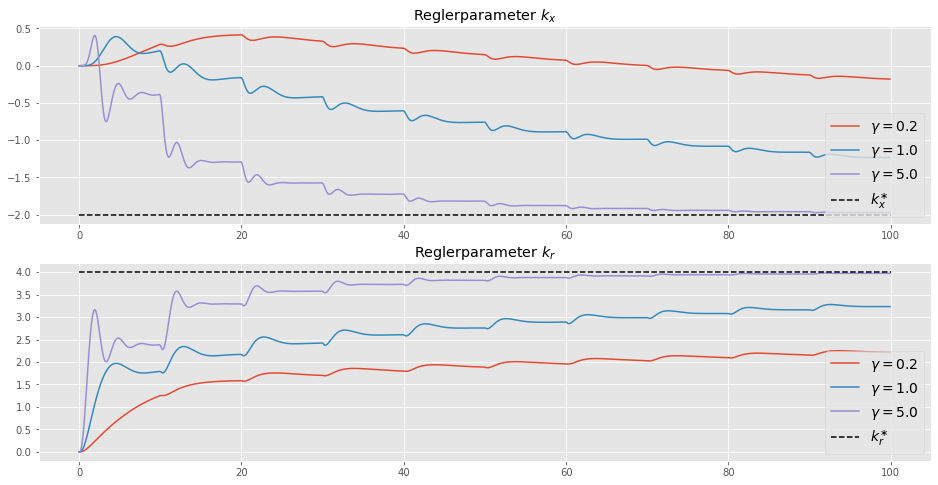
Das Diagramm zeigt, dass die Adaptions-Parameter (\(k_r, k_x\)) für alle drei Adaptions-Verstärkungen (\(\gamma = 0.2, 1.0, 5.0\)) zu den wahren Werten konvergieren, und der Prozessausgang \(x_p\) dem Referenzausgang \(x_r\) folgt, was auch unser Ziel war. Die Konvergenzrate hängt von der Anpassungsverstärkung \(\gamma\) ab. Für kleiner Werte konvergiert der Parameter langsamer. Bei zu großen Werten für \(\gamma\) kann das Adaptionsverfahren instabil werden.
Fazit
Natürlich ist ein System 1. Ordnung mit \(n=1\) sehr eingeschränkt, hat aber in der Praxis trotzdem bereits Anwendungen, insbesondere wenn nichtlineare Modellunsicherheiten vorhanden sind. Dann muss das Verfahren jedoch erweitert werden, was wir in späteren Blogeinträgen noch zeigen werden.
Vorher wollen wir aber noch weitere Grundlagen besprechen. Als nächsten untersuchen wir die Konvergenz des Fehlers und wie diese Konvergenz vom Referenz-Signal \(u_r\) abhängig ist.
Referenzen
- Adaptive Control, Second Editon, 2008 (Karl J. Aström, Björn Wittenmark)
- Model-Reference Adaptive Control: A primer, 2018 (Nhan T. Nguyen)
- Robust Adaptive control, 2012 (Petros A. Ioannou, Jing Sun)
- Deep Model Reference Adaptive Control 2019 (Girish Joshi, Girish Chowdhary)
