Adaptive Regelung - Direct MRAC, MIT Rule, Verstärkung

Wir wollen hier nun ein einfaches Beispiel der Klasse Model-Reference Adaptive Control (MRAC) besprechen. Die MRAC Methoden haben eine große praktische Relevanz, insbesondere in der Luft- und Raumfahrt (Helicopter, Multicopter, Drohnen, Militärjets, …). MRAC ist ein sogenanntes Tracking Problem.

Model-Reference Adpative Control (MRAC)

Erste Varianten von Model-Reference Adpative Control (MRAC) Methoden wurden in den 1950er und 1960er Jahren erarbeitet. Auch werden MRAC Konzepte mit Gauss-Prozessen oder neuronalen Netzen kombiniert. Aus einer Regelungstechnik-Perspektive sind diese Ansätze deswegen attraktiv, weil viele Einsichten der Kontrolltheorie hier weiter verwendet werden können.

Die Idee von MRAC, besteht darin, das gewünschte Verhalten mithilfe eines Referenz-Modells vorzugeben. Ein Regler besitzt nun adaptierbare Parameter, welche so lange verändert werden, bis der reale Ausgang dem Modellausgang entspricht.

MIT Rule

Wir betrachten einen geschlossenen Regelkreis, wo der Regler anpassbare Parameter \(\theta\) besitzt. Das gewünschte Verhalten des geschlossenen Regelkreises wird mithilfe eines Referenz-Modells spezifiziert, dessen Ausgang mit \(y_r\) bezeichnet wird. Nun können wir einen Fehler \(e = y_r - y_p\) einführen, welcher die Differenz zwischen dem Modellausgang \(y_r\) und dem Prozessausgang \(y_p\) misst.

Eine Möglichkeit besteht darin, die Parameter \(\theta\) so anzupassen, dass das Gütefunktional

\[ J(\theta) = \frac{1}{2}e^2 \]

minimiert wird. Um \(J\) kleiner zu machen ist es sinnvoll, die Parameter in Richtung des negative Gradienten von \(J\) anzupassen, sodass gilt

\[ \frac{d\theta}{dt} = - \gamma \frac{\partial J}{\partial \theta} = - \gamma e \frac{\partial e}{\partial \theta} \]

Dieses Adaptionsgesetzt wird als MIT Rule bezeichnet, und geht auf ein Labor am Massachusetts Institute of Technology (MIT) zurück. Die partielle Ableitung \(\dfrac{\partial e}{\partial \theta}\) wird als Sensitivitätsableitung (sensitivity derivative) bezeichnet, und beschreibt den Einfluss der Parameter auf den Fehler.

Direct MRAC: Adaption der Verstärkung

Im Folgendem betrachten wir ein Problem, wo nur eine Verstärkung adaptiert werden soll. Es ist wohl das einfachste MRAC-Problem. Es sei angenommen, dass ein linearer Prozess \(bG(s)\) gegeben ist, wobei \(G(s)\) eine bekannte Übertragungsfunktion und \(b\) ein unbekannter Parameter ist.

Weiters sei das Referenz-Modell \(G_r(s) = b_rG(s)\) gegeben. Mithilfe des Referenz-Eingangs \(u_r\) und dem Referenz-Modell \(G_r(s)\) wird der Modellausgang \(y_r\) erzeugt. Das Problem ist nun, einen Regler zu finden, der dem Modellausgang \(y_r\) folgt. Mit dem Steuerungsgesetz

\[ u_p = \theta u_r \]

ergibt sich für den Ausgang \(y_p(t) = \theta b G(p) u_r(t)\), wobei \(p = \dfrac{d}{dt}\) ein differential Operator ist. Diese Übertragungsfunktion ist gleich zu \(G_r(s) = b_rG(s)\), wenn für den adaptiven Parameter

\[ \theta = \frac{b_r}{b} \]

gilt.

Für diesen Fall stimmt der Ausgang \(y_p\) der realen Strecke mit dem Ausgang \(y_r\) des Modells überein. Wir wollen das MIT-Gesetzt anwenden, um eine Anpassungsmethode herzuleiten.

Abbildung 1: Direct MRAC

Der Fehler ist mit

\[ e = y_r - y_p = + b_rG(p)u_r - b G(p) \theta u_p \]

gegeben, wobei \(u_r\) als das Referenz-Eingangssignal, \(y_r\) als der Modellausgang, \(y_p\) als der Prozessausgang und \(\theta\) als der Anpassungsparameter bezeichnet wird.

Die Sensitivitätsableitung ist mit

\[ \frac{\partial e}{\partial \theta} = - bG(p)u_p = - \frac{b}{b_r} y_r \]

gegeben. Hier wurden die Beziehungen \(y_r = b G(p) \theta u_p\) und \(\theta= \dfrac{b_r}{b}\) genutzt, welche für \(e = 0\) gelten.

Das Adaptionsgesetz ergibt sich nun zu

\[ \frac{d \theta}{d t} = \gamma^{\prime} \frac{b}{b_r} y_r e = \gamma y_r e \cdot \text{sign}(b) \]

mit \(\gamma = \gamma^{\prime} \dfrac{b}{b_r}\) . Das Adaptionsgesetz ist somit unabhängig von dem unbekannten Parameter \(b\), das Vorzeichen muss jedoch bekannt sein.

Tipp

Die zeitliche und bildliche Darstellungen wollen wir hier nicht vermischen. Deshalb haben wir hier neben der Laplace-Variable \(s\) auch einen Differential-Operator \(p\) eingeführt.

Laplace-Variable \(s\)

Gegeben sei die Übertragungsfunktion

\[ G(s) = \dfrac{1}{s+1} = \dfrac{Y(s)}{U(s)} \]

welche auf die Gleichung

\[ sY(s)+Y(s) = U(s) \]

überführt werden kann.

Differential-Operator \(p\)

Um die Übertragungsfunktion für zeitliche Signale nutzen zu können, verwenden wir den Differential-Operator \(p\). Sowohl \(p\) als auch \(G(p)\) können auf zeitliche Signale angewendet werden, so gilt

\[ y(t) = G(p)(u(t)). \]

Aus

\[ G(p) = \dfrac{1}{p+1} = \dfrac{y(t)}{u(t)} \]

ergibt sich die Gleichung

\[ py(t)+y(t) = \dot{y}(t)+y(t) = u(t). \]

Je nach Kontext bedeutet ein klein geschriebene Variable \(y\) entweder \(y=y(t)\) oder \(y=Y(s)\). Das reduziert die Notation und wird auch in der Literatur verwendet.

Beispiel

Mithilfe von python-control können wir die Regelung implementieren und testen.

Das obige Beispiel soll hier nun implementiert werden. Das Problem sei gegeben durch:

• \(G(s) = \frac{1}{s +1}\) (bekannt)
• \(b = 1\) (unbekannt)
• \(b_r = 2\) (bekannt, da vorgegeben)
• \(\lambda = 0.5, 1. ,2.\) (Adaptions-Verstärkung)
• \(u_r = \sin(0.4 \pi t)\) (Referenz-Signal)

Das Modell $G_r(s) = b_rG(s) = = $ könnten wir in das Zustandsmodell

\[ \dot{y}_r = - y_r + b_r u_r \]

überführen. Wir werden aber weiter die Übertragungsfunktion nutzen.

import numpy as np
import matplotlib.pyplot as plt
plt.style.use('ggplot')

import control as ct

Die Strecke ist ein lineares System für welches wir die Klasse control.LinearIOSystem nutzen können.

# linear system
b = 1
s = ct.tf('s')
G_plant_tf = b/(1 + s)

# io model
io_plant = ct.LinearIOSystem(
    G_plant_tf,
    inputs=('up'),
    outputs=('yp'),
    states=('xp'),
    name='plant'
)

Das Referenzmodell ist ein lineares System für welches wir die Klasse control.LinearIOSystem nutzen können.

# linear system
br = 2
G_model_tf = br/(1 + s)

# io model
io_ref_model = ct.LinearIOSystem(
    G_model_tf,
    inputs=('ur'),
    outputs=('yr'),
    states=('xr'),
    name='ref_model'
)

Weil viele Adaptionsgesetze nichtlineare Funktionen sind, wollen wir die Klasse control.NonlinearIOSystem benutzen.

Diese Klasse erlaubt eine Implementation eines nichtlineares Systems der Form

\[ \begin{split} \dot{x} &= f(t, x, u; p) \\ y &= g(t, x, u; p) \\ \end{split}. \]

Dafür werden zwei Funktionen für \(f(t,x,u;p)\) und \(g(t,x,u;p)\) benötigt, welche der Klasse übergeben werden.

def adaptive_controller_state(t, x, u, params):
    """Internal state of adpative controller, f(t,x,u;p)"""
    
    # parameters
    gam = params["gam"] # adaptation gain, aka. learning rate
    signb = params["signb"]

    # controller inputs
    ur = u[0]
    yp = u[1]
    yr = u[2]

    # controller states
    # theta = x[0] # is not needed here
    
    # algebraic relationships
    e = yr - yp

    # dynamics xd = f(x,u)
    d_theta = gam*yr*e*signb
    
    return [d_theta]

def adaptive_controller_output(t, x, u, params):
    """Algebraic output from adaptive controller, g(t,x,u;p)"""

    # controller inputs
    ur = u[0]
    yp = u[1]
    yr = u[2]
    
    # controller state
    theta = x[0]

    # control law
    up = theta*ur

    return [up, theta]

params={"gam":1,"signb":np.sign(b)}

io_controller = ct.NonlinearIOSystem(
    adaptive_controller_state,
    adaptive_controller_output,
    inputs=3,
    outputs=('up', 'theta'),
    states=1,
    params=params,
    name='control',
    dt=0
)

Die drei Blöcke können mit control.InterconnectedSystem zu einem System verbunden werden.

io_closed = ct.InterconnectedSystem(
    (io_plant, io_ref_model, io_controller),
    connections=(
        ('plant.up', 'control.up'),
        ('control.u[1]', 'plant.yp'),
        ('control.u[2]', 'ref_model.yr')
    ),
    inplist=('control.u[0]', 'ref_model.ur'),
    outlist=('plant.yp', 'ref_model.yr', 'control.up', 'control.theta'),
    dt=0
)

# set initial conditions
X0 = np.zeros((3, 1))
X0[0] = 0 # state of system
X0[1] = 0 # state of ref_model
X0[2] = 0 # state of controller

# set simulation duration and time steps
Tend = 20
dt = 0.1

# define simulation time span 
t_vec = np.arange(0, Tend, dt)
# define control input
uc_vec = np.zeros((2, len(t_vec)))
sin = np.sin(0.3 * np.pi * t_vec)
uc_vec[0, :] = sin
uc_vec[1, :] = uc_vec[0, :]

# simulate the system, with different gammas
tout1, yout1 = ct.input_output_response(io_closed, t_vec, uc_vec, X0, params={"gam":0.5})
tout2, yout2 = ct.input_output_response(io_closed, t_vec, uc_vec, X0, params={"gam":1})
tout3, yout3 = ct.input_output_response(io_closed, t_vec, uc_vec, X0, params={"gam":2})

plt.figure(figsize=(16,8))
plt.subplot(2,1,1)
plt.plot(tout2, yout1[0,:], label=r'$y_{\gamma = 0.5}$')
plt.plot(tout2, yout2[0,:], label=r'$y_{\gamma = 1.0}$')
plt.plot(tout3, yout3[0,:], label=r'$y_{\gamma = 2.0}$')
plt.plot(tout1, yout1[1,:] ,label=r'$y_{soll}$', linestyle="--")
plt.legend(fontsize=14)
plt.title('Systemantworten')
plt.subplot(2,1,2)
plt.plot(tout1, yout1[2,:], label=r'$\gamma = 0.5$')
plt.plot(tout2, yout2[2,:], label=r'$\gamma = 1.0$')
plt.plot(tout3, yout3[2,:], label=r'$\gamma = 2.0$')
plt.legend(loc=4, fontsize=14)
plt.title(r'Regler $u_p$')
plt.show()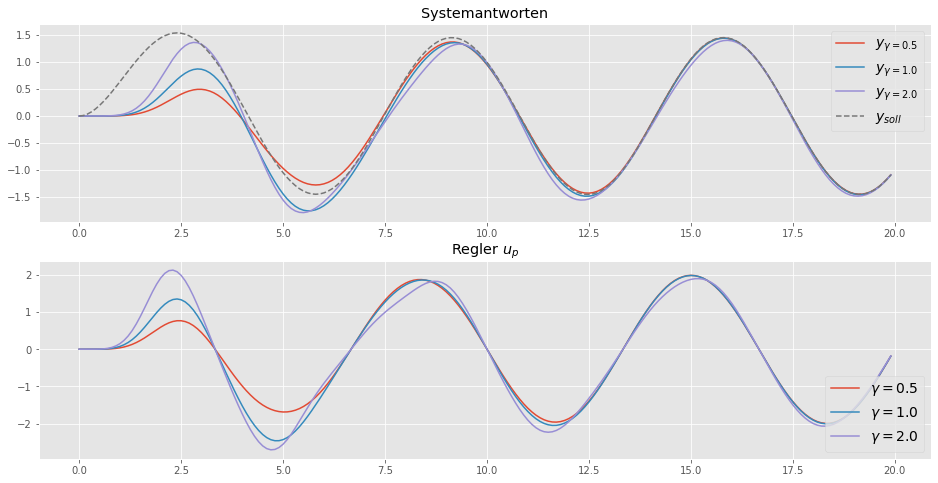

plt.figure(figsize=(16,8))
plt.plot(tout1, yout1[3,:], label=r'$\gamma = 0.5$')
plt.plot(tout2, yout2[3,:], label=r'$\gamma = 1.0$')
plt.plot(tout3, yout3[3,:], label=r'$\gamma = 2.0$')
plt.legend(loc=4, fontsize=14)
plt.title(r'Adaptionsparameter $\theta$')
plt.show()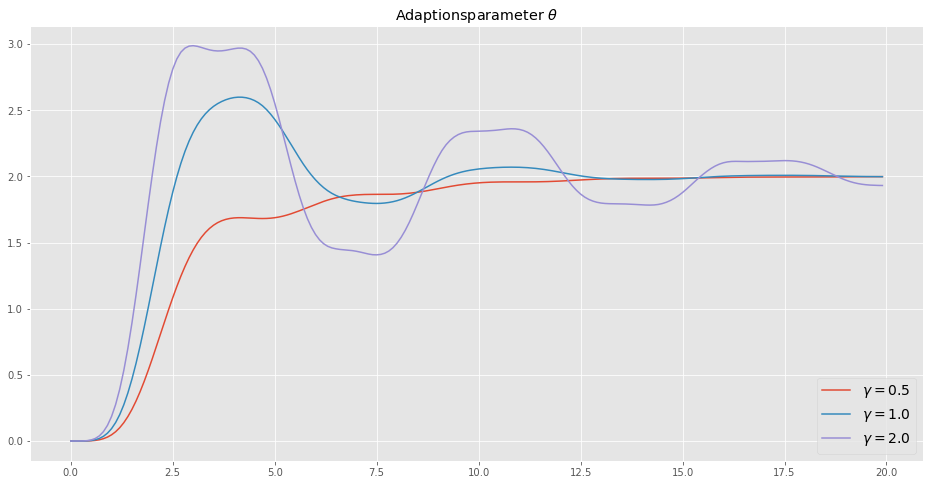

Das Diagramm zeigt, dass der Parameter für \(\gamma = 1\) zum wahren Wert konvergiert, und der Ausgang \(y_p\) dem Modellausgang \(y_r\) folgt, was auch unser Ziel war. Die Konvergenzrate hängt von der Anpassungsverstärkung \(\gamma\) ab. Für kleiner Werte konvergiert der Parameter langsamer. Anpassungsverstärkungen basierend auf den Gradientenabstieg können wie Lernraten nie beliebig groß gewählt werden, da sonst womöglich Instabilitäten auftreten.

Hinweis

In der adaptiven Regelung ist es aber nicht immer notwendig, dass die Parameter zu einem wahren Wert konvergieren. Das ist eine der großen Einsichten der adaptiven Regelung. Wenn der Ausgang \(y_p\) schon perfekt dem Referenz-Ausgangssignal folgt, dann gilt \(e=0\) und der Parameter \(\theta\) würde nicht weiter angepasst, selbst wenn noch ein Parameterfehler \(\tilde{\theta}=\theta^{*}-\theta \neq 0\) vorhanden wäre.

Fazit

Autonome Systeme wie mobile Roboter, Drohnen oder selbstfahrende Autos treffen unweigerlich auf Umgebungen, welche entweder unbekannt oder veränderlich sind. Das verlangt von autonomen Systemen eine Anpassungsfähigkeit auf veränderte Umstände. Die adaptive Regelung und das bestärkende Lernen sind zwei Kandidaten, um dieses Ziel zu erreichen.

Aber auch andere Systeme müssen zunehmend adaptiv gestaltet werden. Denken wir nur an die Stromerzeugung durch erneuerbaren Energien und die zunehmende Elektrifizierung des Verkehrssektors wie auch der Industrie. Statische, das heißt nicht adaptive oder lernende Regelungskonzepte sind dort zunehmend, als hinderlich anzusehen. Adaptive Verfahren müssen dabei Garantien hinsichtlich Stabilität, aber auch Robustheit liefern, um eine Freigabe für kritische Systeme zu erhalten.

Referenzen

• Adaptive Control, Second Editon, 2008 (Karl J. Aström, Björn Wittenmark)
• Model-Reference Adaptive Control: A primer, 2018 (Nhan T. Nguyen)
• Robust Adaptive control, 2012 (Petros A. Ioannou, Jing Sun)
• Deep Model Reference Adaptive Control 2019 (Girish Joshi, Girish Chowdhary)