import numpy as np
import scipy
import scipy.signal as signal
import matplotlib.pyplot as plt
plt.style.use('ggplot')In diesem Blogeintrag wollen wir eine modellfreie Methode besprechen. In der Literatur werden Versionen dieser Methode als Least Squares Policy Iteration besprochen.
Regler Iteration - Datenbasierter Q-Faktor
Gegeben sein ein lineares System
\[ x_{k+1}=Ax_k+Bu_k \]
mit der quadratischen Kostenfunktion
\[ c(x_k,u_k)=x_k^TQx_k+u_k^TRu_k. \]
Die Bellman Gleichung für die \(\mathcal{Q}\)-Funktion und den Regler \(u=-Kx\) lautet
\[ \mathcal{Q}_K(x_{k},u_{k}) = c(x_{k},u_{k}) + \mathcal{Q}_K(x_{k+1},u_{k+1}). \]
Die \(\mathcal{Q}\)-Funktion (\(H\) Matrix) wollen wir hier rein aus Daten lernen. Für ein einfachere Schreibweise führen wir eine neue Koordinate \(z_k = (x_k,u_k)\) ein, womit die Bellman Gleichung für die \(\mathcal{Q}\)-Funktion mit
\[ \mathcal{Q}(z_{k}) = c(z_{k}) + \mathcal{Q}(z_{k+1}) \]
gegeben ist.
Die quadratische \(\mathcal{Q}\)-Funktion
\[ \mathcal{Q}(z_{k}) = z_{k}^T H z_{k} = \phi(z_{k}^T) h \]
kann auch mit linearen Parametern \(h\) und nichtlinearen Basisfunktionen \(\phi(z_{k})^T\) angeschrieben werden.
Diese Umschreibung können wir durch das Kronecker-Produkt
\[ \mathcal{Q}(z_{k}) = z_{k}^T H z_{k} = (z_{k} \otimes z_{k})^T vec(H) = vec(z_{k}^Tz_{k})^T vec(H) = \phi(z_{k})^T h \]
mathematisch exakt durchführen.
Für einen einzelnen Datenpunkt lautet die Bellman Gleichung somit
\[ \phi(z_{k})^T h = c(z_{k}) + \phi(z_{k+1})^T h \]
und für \(p\)-Datenpunkte erhalten wir eine Matrixgleichung
\[ \begin{split} \underset{\Phi(z_k)} {\underbrace{\begin{bmatrix} \phi(z_{k})^T \\ \phi(z_{k+1})^T \\ \vdots \\ \phi(z_{k+p})^T \end{bmatrix}}} h &= \underset{C(z_k)} {\underbrace{\begin{bmatrix} c(z_{k})^T \\ c(z_{k+1})^T \\ \dots \\ c(z_{k+p})^T \end{bmatrix}}} + \underset{\Phi(z_{k+1})} {\underbrace{\begin{bmatrix} \phi(z_{k+1})^T \\ \phi(z_{k+2})^T \\ \vdots \\ \phi(z_{k+p+1})^T \end{bmatrix}}} h \end{split} \]
welche wir für die Bestimmung von \(h\) nutzen können.
Zum Lösen dieser Gleichung kann eine Regler Iteration (engl. policy iteration) oder eine Werte Iteration (engl. value iteration) einsetzen.
Regler Iteration
Für die Regler Iteration lautet das zu lösende Gleichungssystem
\[ \left( \Phi(z_k) - \Phi(z_{k+1}) \right) h = C(z_k). \]
LS - Least Squares
Das obige Gleichungssystem kann am einfachsten mit Hilfe des LS (Least Squares) Schätzers
\[ h = \left( \left( \Phi(z_k) - \Phi(z_{k+1}) \right)^T \left( \Phi(z_k) - \Phi(z_{k+1}) \right) \right)^{-1} \left( \Phi(z_k) - \Phi(z_{k+1}) \right)^T C(z_k) \]
gelöst werden.
LSTDQ - Least Squares Temporal Differenz Q
Gängiger ist aber der LSTDQ (Least Squares Temporal Differenz Q) Schätzer
\[ h = \left( \Phi(z_k)^T \left( \Phi(z_k) - \Phi{z_{k+1}} \right) \right)^{-1} \Phi(z_k)^T C(z_k). \]
Dieser Schätzer basiert auf der Idee der IV-Schätzung (Instrumentvariablenschätzung, Methode der Instrumentvariablen). Bei einer Regressionsanalyse zielt die IV-Methode darauf, eine Korrelation zwischen erklärenden Variablen und dem Fehlerterm auszuschließen. Diese Methode kommt aus der schließenden Statistik und findet auch breite Anwendung in der Systemidentifikation und der adaptiven Regelung.
Werte Iteration
Für die Werte Iteration muss die Gleichung
\[ \Phi(z_k) h_{j+1} = C(z_k) + \Phi(z_{k+1}) h_j \]
gelöst werden.
LS - Least Squares
Wiederum können die Parameter mit Hilfe des LS (Least Squares) Schätzers
\[ h_{j+1} = \left( \Phi(z_k)^T \Phi(z_k) \right)^{-1} \Phi(z_k)^T \left( C(z_k) + \Phi(z_{k+1}) h_j \right) \]
gelernt werden.
Implementierungsvarianten
Es gibt nun noch ein paar weitere Implementierungsvarianten zu beachten. Im bestärkenden Lernen gibt es oft 2 Regler, der Regler der mit dem System interagiert und die Daten erzeugt (Behaviour / Play Policy \(u_{play}\)) und der Regler (Target Policy \(u_{targ}\)) der gelernt werden soll.
Die beiden Regler sind im Allgemein verschieden \(u_{play} \neq u_{targ}\) (off-policy) können aber auch zusammenfallen \(u_{play} == u_{targ}\) (on-pollicy).
Wählt man
\[ u_{play} = u_{targ} = u_k = - K x_k + v_k \]
dann kann die obige Regler-Iteration mit
\[ h = \sum_{i=0}^{T-1}\phi(x_i,u_i) \left( \phi(x_i,u_i)-\phi(x_{i+1},u_{i+1}) \right)^{-1} \left( \sum_{i=0}^{T-1} \phi(x_i,u_i)c(x_i,u_i) \right) \]
gelöst werden. Allerdings zeigt sich dass dies nur mit einen vernünftigen gaußischen Explorationsrauschen \(v_k ~ \mathbb{N}(0,\Sigma)\) funktioniert. Für ein generelles Explorationsrauschen \(v_k\) verwenden wir den Schätzer
\[ h = \sum_{i=0}^{T-1}\phi(x_i,u_i) \left( \phi(x_i,u_i)-\phi(x_{i+1}, - K x_{k+1} ) \right)^{-1} \left( \sum_{i=0}^{T-1} \phi(x_i,u_i)c(x_i,u_i) \right) \]
wo \(u_{play} = u_k = - K x_k + v_k\) ein stochastischer Regler und \(u_{targ} = u_k = - K x_k\) ein deterministischer Regler ist. Dennoch wird auch hier von On-Policy gesprochen, weil beide Regler im Kern noch \(K\) verwenden.
Im Off-Policy Fall werden für die beiden Regler \(u_{play} = u_k = - K_0 x_k + v_k\) und \(u_{targ} = u_k = - K x_k\) unterschiedliche Reglermatrizen verwendet.
Kleinste Quadrate Regler Iteration (Online, On-Policy)
(engl. Least Squares Policy Iteration (Online, On-Policy))
Algorithmus
Annahmen
- Unbekannte Kostenfunktion (R,Q), nur c kann gemessen werden
- Unbekanntes Dynamisches Model (A,B), nur x kann gemessen werden
- Regler-Iteration beinhaltet die Lösung der Lyapunov Gleichung.
- benötigt einen stabilisierenden Regler \(K_j\) in jedem Iteration-Schritt
- Daten werden online mit \(K_j\) gesammelt. (Online, On-Policy)
Initialisierung: - \(K_0\) Auswahl eines zulässigen (z.B. stabilisierend) Reglers - \(T\) Länge der Ausrollung, Anzahl der Datenpunkte - \(N\) maximale Anzahl der Regler Iterationen - \(\epsilon\) Schranke, Konvergenz - \(\sigma_n^2\) Explorations-Varianz —
- for \(j=0,...N-1\) do
- Collect Data \(D=\{(x_k,u_k,x_{k+1})\}_{k=0}^{T}\) with \(u_k = - K_j x_k + \eta_k, \eta_k \sim \mathcal{N}(0,\sigma_n^2I)\)
- \(H_j = EstimateQ(D,K_j)\) with full update \(W_{j+1}^{T}(\phi(z_k)-\phi(z_{k+1})) = c(x_k,u_k)\)
- \(K_{j+1} = G \left( H_j \right)\)
- if \(\left\Vert H_j-H_{j-1} \right\Vert < \epsilon\) then break
- end for
- \(H_{j+1} = EstimateQ(D,K_{j+1})\)
- return \(K_{j+1}, H_{j+1}\)
Implementierung
m1 = 1
d1 = 0.15
c1 = 0.3
m2 = 1
d2 = 0.15
c2 = 0.3
d3 = 0.15
c3 = 0.3
A = np.array([[0., 0., 1., 0.],
[0., 0., 0., 1.],
[-(c1+c2)/m1, c2/m1, -(d1+d2)/m1, d2/m1],
[c2/m2, -(c2+c3)/m2, (d2)/m2, -(d2+d3)/m2]])
B = np.array([[0., 0.], [0., 0.], [1./m1, 0.], [0., 1/m2]])
C = np.array([[1., 0., 0., 0], [0., 1., 0., 0.]])
D = np.array([[0., 0.],[0., 0.]])sys_c = signal.StateSpace(A, B, C, D)
dt = 0.1
sys_d = sys_c.to_discrete(dt)eig_values_c = np.linalg.eigvals(sys_c.A)
eig_values_carray([-0.225+0.92161543j, -0.225-0.92161543j, -0.075+0.54256336j,
-0.075-0.54256336j])eig_values_d = np.linalg.eigvals(sys_d.A)
eig_values_darray([0.97360179+0.08998355j, 0.97360179-0.08998355j,
0.99106754+0.05382452j, 0.99106754-0.05382452j])R = np.eye(2)*1
Q = np.eye(4)*10plt.plot(np.real(eig_values_d),np.imag(eig_values_d), 'go')
draw_circle = plt.Circle((0.0, 0.0), 1.0, color='red', fill=False, linewidth=2.0)
plt.gcf().gca().add_artist(draw_circle)
plt.axis('equal')
plt.xlim(-2, 2)
plt.ylim(-2, 2)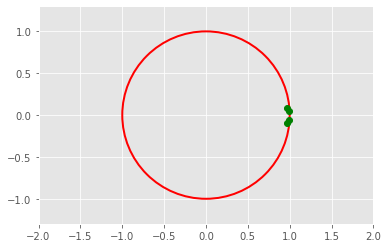
Code: LQR Riccati Lösung
def dlqr(A,B,Q,R):
""" solve LQR problem
returns: controller, value function, closed loop eigenvalues
"""
#first, try to solve the ricatti equation
P = np.matrix(scipy.linalg.solve_discrete_are(A, B, Q, R))
#compute the LQR gain
K = np.matrix(scipy.linalg.inv(B.T@P@B+R)@(B.T@P@A))
eigVals, eigVecs = scipy.linalg.eig(A-B@K)
return K, P, eigValsCode: LQR Offline Regler Iteration
def get_Qfunction(A, B, Q, R, P):
""" calc Q function => H from model + value function
returns: Q function, controller
"""
n, p = B.shape
H1 = np.hstack((Q+A.T@P@A, A.T@P@B))
H2 = np.hstack((B.T@P@A, R+B.T@P@B))
H = np.vstack((H1,H2))
H_uu = H[n:,n:]
H_ux = H[n:,:n]
K = np.linalg.inv(H_uu)@H_ux
return H, K
def svec(H):
Nx,Ny = H.shape
index_triu = np.triu_indices(Nx)
W = H[index_triu]
return W, Nx
def smat(W, Nx):
index_triu = np.triu_indices(Nx)
Htri = np.zeros((Nx, Nx))
Htri[index_triu] = W
H = Htri + Htri.T - np.diag(np.diag(Htri))
return H
def svec2(H):
Nx,Ny = H.shape
index_triu = np.triu_indices(Nx)
H2 = H + np.triu(H,1)
W = H2[index_triu]
return W, Nx
def smat2(W, Nx):
index_triu = np.triu_indices(Nx)
Htri = np.zeros((Nx, Nx))
Htri[index_triu] = W
H = Htri/2 + (Htri.T)/2
return Hdef generate_data(A,B,K0,x0,T,noise):
n, p = B.shape
X_data = np.zeros((T+1,n,1))
U_data = np.zeros((T,p,1))
x = x0
for i in range(0,T):
# interaction with the system
## play policy, behavior policy
u = - K0 @ x + noise * np.random.randn(p).reshape(p,1)
X_data[i,:] = x
U_data[i,:] = u
## state update
xn = A @ x + B @ u
## shift state
x = xn
X_data[T,:] = x
return X_data, U_datadef estimate_H(X_data, U_data, Ki, num_of_para, modeH='LS'):
debug = False
T = X_data.shape[0]
phi_z_vec = np.zeros((num_of_para,T))
phi_zn_vec = np.zeros((num_of_para,T))
target_vec = np.zeros((1,T))
for k in range(0,T-1):
x = X_data[k,:,:]
xn = X_data[k+1,:,:]
u = U_data[k,:,:]
## target policy, evualating policy
un = - Ki @ xn # virutal next input
# collect values for LSQ
## phi_k
z = np.row_stack([x, u])
new_phi_z, Nz = svec(z@z.T)
phi_z_vec = np.roll(phi_z_vec,-1, axis=1)
phi_z_vec[:,-1] = new_phi_z
## phi_{k+1}
zn = np.row_stack([xn, un])
new_phi_zn, _ = svec(zn@zn.T)
phi_zn_vec = np.roll(phi_zn_vec,-1, axis=1)
phi_zn_vec[:,-1] = new_phi_zn
## target
new_target = x.T @ Q @ x + u.T @ R @ u
target_vec = np.roll(target_vec,-1)
target_vec[:,-1] = new_target
delta_phi = phi_z_vec - phi_zn_vec
if modeH == "LS":
MA = delta_phi @ delta_phi.T
Mb = target_vec @ delta_phi.T
else:
# LSTDQ
MA = delta_phi @ phi_z_vec.T
Mb = target_vec @ phi_z_vec.T
W = Mb @ np.linalg.inv(MA)
H = smat2(W, Nz)
H = smat2(W, Nz)
return Hdef estimate_K(H):
H_uu = H[n:,n:]
H_ux = H[n:,:n]
K = np.linalg.inv(H_uu)@H_ux
return Kdef Q_Factor_LSPI_Version3(A,B,Q,R,K0,x0,N,T,noise,modeH='LS'):
debug=None
n, p = B.shape
pn = p+n
num_of_para = int(pn*(pn+1)/2)
print("Number of Parameters:", num_of_para)
if (T < num_of_para+1):
print(num_of_para)
print(T)
assert print("T is not long enough")
Ki = K0
K_list = []
H_list = []
K_list.append(Ki)
for i in range(0,N):
X_data, U_data = generate_data(A,B,Ki,x0,T,noise)
Hi = estimate_H(X_data, U_data, Ki, num_of_para, modeH)
Ki = estimate_K(Hi)
H_list.append(Hi)
K_list.append(Ki)
K = Ki
H = estimate_H(X_data, U_data, K, num_of_para)
H_list.append(Hi)
return K, H, K_list, H_listRiccati Lösung
n, p = sys_d.B.shape
R = np.eye(p)
Q = np.eye(n)K_infinite, P_infinite, eigVals_closed = dlqr(sys_d.A,sys_d.B,Q,R)
K_infinitematrix([[0.52591444, 0.14589589, 1.15336362, 0.20646134],
[0.14589589, 0.52591444, 0.20646134, 1.15336362]])H_infinite, K_infinite_ = get_Qfunction(sys_d.A,sys_d.B,Q,R,P_infinite)
print("Regler sind gleich : ", np.allclose(K_infinite,K_infinite_))Regler sind gleich : TrueRegler Iteration für LQR
# initial policy is needed
n,p = sys_d.B.shape
Ac_eig = np.arange(0,0.1,0.1/n) +0.5
fsf1 = signal.place_poles(sys_d.A, sys_d.B, Ac_eig)
K0 = fsf1.gain_matrix
K0array([[21.06759499, 1.30711111, 7.97758729, 0.29670384],
[ 1.3071133 , 21.06786057, 0.29670422, 7.97763139]])# initial state
n,p = sys_d.B.shape
mean = np.zeros((n,1)).flatten()
cov = np.eye(n)
x0 = np.random.multivariate_normal(mean, cov, 1).T
x0array([[-1.19888095],
[-0.9414457 ],
[ 0.62646727],
[ 0.10309504]])# LS
T = 30
N = 100
noise = 1
K_Q_PI, H_Q_PI, K0_list, H0_list = Q_Factor_LSPI_Version3(sys_d.A,sys_d.B,Q,R,K0,x0,N,T,noise,modeH="LSTDQ")
K_Q_PI
print("Regler - RI Init : ", K0)
print("Regler - RI End : ", K_Q_PI)
print("Regler - Riccati : ", K_infinite)
print("Regler sind gleich : ", np.allclose(K_infinite,K_Q_PI))
print("Werte Funktionen sind gleich : ", np.allclose(H_infinite,H_Q_PI))Number of Parameters: 21
Regler - RI Init : [[21.06759499 1.30711111 7.97758729 0.29670384]
[ 1.3071133 21.06786057 0.29670422 7.97763139]]
Regler - RI End : [[0.52591444 0.14589589 1.15336362 0.20646134]
[0.14589589 0.52591444 0.20646134 1.15336362]]
Regler - Riccati : [[0.52591444 0.14589589 1.15336362 0.20646134]
[0.14589589 0.52591444 0.20646134 1.15336362]]
Regler sind gleich : True
Werte Funktionen sind gleich : TrueK_array = np.array(K0_list).squeeze()
H_array = np.array(H0_list).squeeze()
K_delta_norm = np.zeros(K_array.shape[0])
H_delta_norm = np.zeros(H_array.shape[0])
for i in range(0,K_array.shape[0]):
K_delta_norm[i] = np.linalg.norm(K_array[i] - K_infinite)
H_delta_norm[i] = np.linalg.norm(H_array[i] - H_infinite)
plt.figure(figsize=(12,6))
plt.subplot(1,2,1)
plt.plot(K_delta_norm)
plt.xlabel('iteration')
plt.ylabel(r'$\left\Vert K*-K \right\Vert$',usetex=True)
plt.subplot(1,2,2)
plt.plot(H_delta_norm)
plt.xlabel('iteration')
plt.ylabel(r'$\left\Vert H*-H \right\Vert$',usetex=True);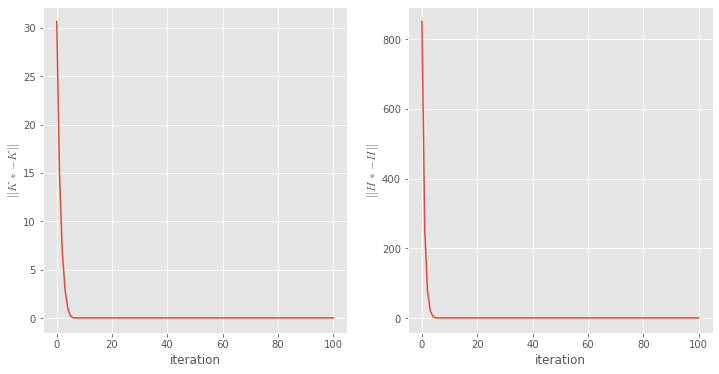
Fazit
\(\mathcal{Q}\)-Faktor Methoden sind eine wichtige Klasse von BL Methoden. Es gibt viele Implementierungsvarianten, wobei das \(\mathcal{Q}\)-Lernen sicher die Bekannteste ist. Im Prinzip funktionieren Methoden des Deep Reinforcement Learning sehr ähnlich, jedoch wird dort die \(\mathcal{Q}\)-Funktion durch ein tiefes neuronales Netz parametriert. Für das LQR Problem sind \(\mathcal{Q}\)-Faktor Methoden durchaus dateneffizient. Das Identifizieren der Dynamik und das anschließende Lösen der Riccati Gleichung ist jedoch die dateneffizienteste Methoden für das LQR Problem.
Python
Wir haben an Hand des Masse-Feder-Systems einige Methoden der technischen Kybernetik kennengelernt. Alles wurde in Python implementiert. Deshalb werden wir uns in den nächsten Monaten sehr intensive mit der Programmiersprachen Python befassen.

