Masse Feder System, Reglersynthese durch Polvorgabe

In diesem Notebook wollen wir einen Regler mittels Polevorgabe entwerfen. Dazu benutzen wir die Python-Bibliothek control mit dem Befehl place.

System

\[ \dot{\mathbf{x}} = \mathbf{A}\mathbf{x} + \mathbf{B} \mathbf{u} \]

\[ \begin{bmatrix} \dot{x}_1 \\ \dot{x}_2 \\ \dot{x}_3 \\ \dot{x}_4 \end{bmatrix} = \begin{bmatrix} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ -\frac{c_1+c_2}{m_1} & \frac{c_2}{m_1} & -\frac{d_1+d_2}{m_1} & \frac{d_1}{m_1} \\ \frac{c_2}{m_2} & -\frac{c_2+c_3}{m_2} & \frac{d_2}{m_2} & -\frac{d_2+d_3}{m_2} \end{bmatrix} + \begin{bmatrix} 0 & 0 \\ 0 & 0 \\ \frac{1}{m_1} & 0 \\ 0 & \frac{1}{m_2} \end{bmatrix} \begin{bmatrix} F_1 \\ F_2 \end{bmatrix} \]

Zustandsregler mittels Polvorgabe

Gegeben sei ein lineares System

\[ \dot{x} = Ax + Bu \]

wo \(x \in \mathbb{R}^n\) und \(u \in \mathbb{R}^m\) der Zustand und Eingangsvektor. Das Ziel ist einen Zustandsregler der Form

\[ u = - K x \]

welcher das geschlossen System

\[ \dot{x} = (A-BK)x \]

stabilisiert. Die Theorie der Polvorgabe für MIMO Systeme ist durchaus komplex und soll hier erst einmal nicht dargestellt werden.

import control as ctrl
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('ggplot')

m1 = 1
d1 = 0.0
c1 = 0.3

m2 = 1
d2 = 0.0
c2 = 0.3

d3 = 0.0
c3 = 0.3

A = np.array([[0., 0., 1., 0.],
              [0., 0., 0., 1.], 
              [-(c1+c2)/m1, c2/m1, -(d1+d2)/m1, d2/m1],
              [c2/m2, -(c2+c3)/m2, (d2)/m2, -(d2+d3)/m2]])
B = np.array([[0., 0.], [0., 0.], [1./m1, 0.], [0., 1/m2]])
C = np.array([[1., 0., 0., 0], [0., 1., 0., 0.]])
D = np.array([[0., 0.],[0., 0.]])

sys_c = ctrl.ss(A,B,C,D)

ctrl.pole(sys_c)

array([-2.35922393e-17+0.9486833j , -2.35922393e-17-0.9486833j ,
        5.55111512e-17+0.54772256j,  5.55111512e-17-0.54772256j])

K = ctrl.place(A, B, [-1, -1, -2, -2])

eig_values_c = np.linalg.eigvals(sys_c.A)
eig_values_c

array([-2.35922393e-17+0.9486833j , -2.35922393e-17-0.9486833j ,
        5.55111512e-17+0.54772256j,  5.55111512e-17-0.54772256j])

eig_values_c_cl = np.linalg.eigvals(A-B@K)
eig_values_c_cl

array([-1., -2., -2., -1.])

plt.figure(figsize=(6,4))
plt.plot(np.real(eig_values_c),np.imag(eig_values_c), 'bx', label="Offener Regelkreis")
plt.plot(np.real(eig_values_c_cl),np.imag(eig_values_c_cl), 'gx', label="Geschlossener Regelkreis")
plt.vlines(0,-5,5, color='red', linewidth=1.0)
plt.axis('equal')
plt.xlim(-5, 5) 
plt.ylim(-5, 5)
plt.legend()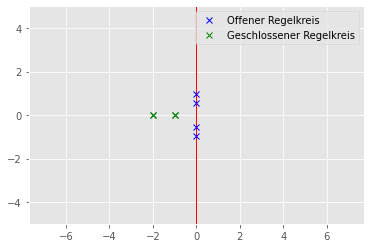

Fazit

Wir haben in diesem Notebook einen Regler entworfen welcher das System stabilisiert. Für größere System ist die Polvorgabe aber wenig geeignet, weil wir nie wissen was gute Pole sind und das einfache Ausprobieren sich nur für kleiner Systeme eignet.

Im Folgenden wollen wir Methoden einführen die auf Optimierungen basieren. Anstatt die Pole per Hand vorzugeben formulieren wir Optimierungsprobleme. Wenn eine Lösung gefunden wird bekommen wir einen Regler geliefert ohne die Dynamik direkt vorzugeben.