import numpy as np
import scipy.signal as signal
import matplotlib.pyplot as plt
import scipy
plt.style.use('ggplot')Eine der bekanntesten Methoden aus dem Gebiet der dynamischen Programmierung ist die modellbasierte Regler-Iteration.
Modellbasierte Offline Regler-Iteration
Regler-Evaluierung
Gegeben sei ein Regler \(K\) dessen Werte Funktion mit
\[ \mathcal{V}_{K}(x_k)=x_k^TP_{K}x_k \]
gegeben ist. Die Bellman Gleichung für einen bestimmten Regler lautet
\[ \mathcal{V}_{K}(x_k) = c(x_k,-Kx_k) + \mathcal{V}_{K}(x_{k+1}) \]
bzw. für das LQR Problem
\[ x_k^TP_{K}x_k = x_k^TQx_k + x_k^TK^TRKx_k + x_{k+1}^TP_{K}x_{k+1}. \]
Die geschlossene Dynamik \(x_{k+1}=(A-BK)x_k\) eingesetzt, ergibt
\[ x_k^TP_{K}x_k = x_k^T(Q+K^TRK+(A-BK)^TP_{K}(A-BK))x_k. \]
Durch das Umstellen der Gleichung und das Weglassen von \(x_k\) erhalten wir die Lyapunov Gleichung
\[ (A-BK)^TP_{K}(A-BK)-P_{K}+Q+K^TRK = 0. \]
Diese Lyapunov Gleichung kann effizient gelöst werden. Die Regler-Evaluierung im LQR Fall ist also durch eine Lyapunov Gleichung gegeben.
Regler-Aktualisierung
Durch die Regler-Evaluierung ist die Werte Funktion \(\mathcal{V}_K(x_k)\) bzw. die Matrix \(P_K\) bekannt. Die Werte Funktion kann nun genutzt werden um eine Verbesserung des Reglers zu erreichen.
Die Herleitung:
\[ \begin{split} u_k &= \underset{u_k}{\text{ arg min }} \left( c(x_k, u_k) + \mathcal{V}_{K}(x_{k+1}) \right) \\ &= \underset{u_k}{\text{ arg min }} \left( c(x_k, u_k) + \mathcal{V}_{K}((Ax_k+Bu_k) \right) \\ &= \underset{u_k}{\text{ arg min }} \left( x_k^{T}Qx_k + u_k^{T}Ru_k + (Ax_k+Bu_k)^TP_{K}(Ax_k+Bu_k) \right) \end{split} \]
\[ \frac{\partial}{\partial u_k} \left( x_k^TQx_k+u_k^TRu_k+(Ax_{k}+Bu_{k})^TP_{K}(Ax_{k}+Bu_{k}) \right) = 0 \]
\[ Ru_k+B^TP_{K}(Ax_k+Bu_k) = 0 \]
\[ u_k = -(R+B^TP_{K}B)^{-1}B^TP_{K}A x_k \]
Der verbesserte Regler kann also mit
\[ K^{\prime} = (R+B^TP_{K}B)^{-1}B^TP_{K}A \]
angegeben werden. Für diesen neuen Regler \(K^{\prime}\) kann nun eine neue Regler-Evaluierung durchgeführt werden, womit die Werte Funktion
\[ \mathcal{V}_{K^{\prime}}(x_k)=x_k^TP_{K^{\prime}}x_k \]
gegeben ist. Dieses Vorgehen kann nun wiederholt werden bis der Regler zum optimalen Regler \(K_{*}\) konvergiert.
- Initialisierung: Auswahl eines zulässige (z.B., stabilisierend) Regler
\[u=K_0 x_k\]
- Regler Evaluierung (Lyapunov Gleichung)
\[ (A-BK_j)^TP_{j+1}(A-BK_j)-P_{j+1}+Q+K_jRK_j = 0 \]
- Regler Aktualisierung
\[ K_{j+1} = (R+B^TP_{j+1}B)^{-1}B^TP_{j+1}A \]
Implementierung
m1 = 1
d1 = 0.15
c1 = 0.3
m2 = 1
d2 = 0.15
c2 = 0.3
d3 = 0.15
c3 = 0.3
A = np.array([[0., 0., 1., 0.],
[0., 0., 0., 1.],
[-(c1+c2)/m1, c2/m1, -(d1+d2)/m1, d2/m1],
[c2/m2, -(c2+c3)/m2, (d2)/m2, -(d2+d3)/m2]])
B = np.array([[0., 0.], [0., 0.], [1./m1, 0.], [0., 1/m2]])
C = np.array([[1., 0., 0., 0], [0., 1., 0., 0.]])
D = np.array([[0., 0.],[0., 0.]])sys_c = signal.StateSpace(A, B, C, D)
dt = 0.1
sys_d = sys_c.to_discrete(dt)eig_values_c = np.linalg.eigvals(sys_c.A)
eig_values_carray([-0.225+0.92161543j, -0.225-0.92161543j, -0.075+0.54256336j,
-0.075-0.54256336j])eig_values_d = np.linalg.eigvals(sys_d.A)
eig_values_darray([0.97360179+0.08998355j, 0.97360179-0.08998355j,
0.99106754+0.05382452j, 0.99106754-0.05382452j])R = np.eye(2)*1
Q = np.eye(4)*10Code: LQR Riccati Lösung
def dlqr(A,B,Q,R):
""" Solve LQR Problem
Returns: Controller, Valute Function, Closed Loop Eigenvalues
"""
#first, try to solve the ricatti equation
P = np.matrix(scipy.linalg.solve_discrete_are(A, B, Q, R))
#compute the LQR gain
K = np.matrix(scipy.linalg.inv(B.T@P@B+R)@(B.T@P@A))
eigVals, eigVecs = scipy.linalg.eig(A-B@K)
return K, P, eigValsCode: LQR Offline Regler Iteration
def solve_discrete_lyapunov(A, Q, method=None):
""" Solves Discrete Lyapunov Equation
A^T P A - P + Q = 0
Returns: Lyapunov Function (Matrix)
"""
P = scipy.linalg.solve_discrete_lyapunov(A.T,Q)
assert np.allclose(A.T.dot(P).dot(A) - P, -Q)
return Pdef policy_evaluation_step(A,B,Q,R,Kj):
""" Policy Evaluation via Lyapunov Equation
(A-B K)...
Returns: Value Functions (Matrix)
"""
Ac = A-B@Kj
Qc = Q+Kj.T@R@Kj
P = solve_discrete_lyapunov(Ac,Qc)
return Pdef policy_improvement_step(A,B,R,Pjp):
""" Policy Improvement
K = (R+B^T P B)^{-1}B^T P A
"""
K = np.linalg.inv(R+B.T@Pjp@B)@B.T@Pjp@A
return Kdef policy_iteration(A,B,Q,R,Kj,n):
""" polic_evaluation + policy_improvement
"""
Pjp = 0
for i in range(0,n):
# Policy evaluation: Solving the lyapunov equation
Pjp = policy_evaluation_step(A,B,Q,R,Kj)
# Policy improvement: Value to Policy
Kjp = policy_improvement_step(A,B,R,Pjp)
Kj = Kjp
K = Kj
P = Pjp
return K, Pplt.plot(np.real(eig_values_d),np.imag(eig_values_d), 'gx')
draw_circle = plt.Circle((0.0, 0.0), 1.0, color='red', fill=False, linewidth=1.0)
plt.gcf().gca().add_artist(draw_circle)
plt.axis('equal')
plt.xlim(-2, 2)
plt.ylim(-2, 2)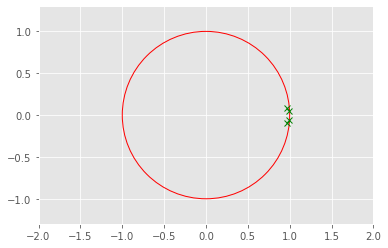
Riccati Lösung
K_infinite, P_infinite, eigVals_closed = dlqr(sys_d.A,sys_d.B,Q,R)
K_infinitematrix([[2.09953908, 0.22634538, 3.08931627, 0.17083531],
[0.22634538, 2.09953908, 0.17083531, 3.08931627]])Regler Iteration für LQR
# Initial policy is need
Ac_eig = [0.5,0.6,0.7,0.8]
fsf1 = signal.place_poles(sys_d.A, sys_d.B, Ac_eig)
K0 = fsf1.gain_matrix
K0array([[11.05073946, 3.76452494, 6.18886334, 0.95206432],
[ 3.76454607, 11.05330907, 0.95206947, 6.1894687 ]])n = 10000
K_j , P_j = policy_iteration(sys_d.A,sys_d.B,Q,R,K0,n)
print("Regler - RI Init : ", K0)
print("Regler - RI End : ", K_j)
print("Regler - Riccati : ", K_infinite)Regler - RI Init : [[11.05073946 3.76452494 6.18886334 0.95206432]
[ 3.76454607 11.05330907 0.95206947 6.1894687 ]]
Regler - RI End : [[2.09953908 0.22634538 3.08931627 0.17083531]
[0.22634538 2.09953908 0.17083531 3.08931627]]
Regler - Riccati : [[2.09953908 0.22634538 3.08931627 0.17083531]
[0.22634538 2.09953908 0.17083531 3.08931627]]Vergleiche die Regler
print("Regler sind gleich : ", np.allclose(K_infinite,K_j))
print("Werte Funktionen sind gleich : ", np.allclose(P_infinite,P_j))Regler sind gleich : True
Werte Funktionen sind gleich : Trueplt.plot(np.real(eig_values_d),np.imag(eig_values_d), 'gx')
plt.plot(np.real(eigVals_closed),np.imag(eigVals_closed), 'bx')
draw_circle = plt.Circle((0.0, 0.0), 1.0, color='red', fill=False, linewidth=1.0)
plt.gcf().gca().add_artist(draw_circle)
plt.axis('equal')
plt.xlim(-2, 2)
plt.ylim(-2, 2)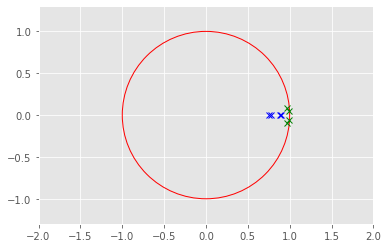
Fazit
Die modellbasierte Regler-Iteration zählt zu den Methoden der Kontrolltheorie, wird aber auch oft in BL-Literatur eingeführt. Anhand des LQR Problems, haben wir eine offline Regler-Iteration durchgeführt und die Lösung mit der Riccati Gleichung verglichen. Die Regler-Evaluierung führt hier auf eine Lyapunov Gleichung welche effizient gelöst werden kann.