Masse Feder System, Reglersynthese durch LMIs

Kontrolltheorie
Autor:in

Johannes Kaisinger

Veröffentlichungsdatum

3. September 2021

Lineare Matrix-Ungleichungen (LMIs = Linear Matrix Inequalities ) haben in den letzten 20 Jahren das Feld der Regelungstechnik enorm beeinflusst. Ihre Bedeutung ist im Bereich der Optimalen und Robusten Regelung kaum zu überschätzen. Dennoch werden diese an Universitäten kaum gelehrt, weil der mathematische Aufwand enorm ist.

Wir wollen in diesem Notebook zeigen das Python den Zugang zu LMIs deutlich erleichtern könnte. Jupyter Notebooks erlauben das Verbinden der mathematischen Theorie mit Programmierbeispielen, was das Lernen anspruchsvoller Techniken enorm erleichtern wird. Der freie Zugang zu Python-Bibliotheken ist ein weiterer Aspekt warum diese Techniken eine weitere Verbreitung finden könnten.

LMIs führen auf konvexe Optimierungsprobleme die mit cvxpy gelöst werden können. Es stehen jedoch weitere Python-Bibliotheken für das Lösen von konvexen Optimierungsproblemen zur Verfügung.

import numpy as np
import cvxpy as cp
import scipy.signal as signal

import matplotlib.pyplot as plt
plt.style.use('ggplot')

Stabilität linearer Systeme

Betrachten wir ein lineares System

\[ \dot{x} = Ax, x(0) = x_0 \]

wo \(x \in \mathbb{R}^n\). Die einzige Ruhelage des Systems ist \(x_R = 0\). Der Kandidat einer Lyapunov Funktion ist mit

\[ V(x) = x^TPx \]

gegeben wobei \(P \in \mathbb{R}^{n\times n}\) eine positive definite Matrix ist und sich somit \(V(x)>0\) für $x $ ergibt. Das lineare System ist stabil, wenn eine Matrix \(P>0\) existiert welches die Ungleichung

\[ \dot{V}(x) = (Ax)^TPx+x^TPAx < 0 \]

erfüllt. Für lineare Systeme ist die Existenz einer Lyapunov Funktion eine notwendige und hinreichende Stabilitätsbedingung. Diese Bedingung kann nun mit Hilfe von linearen Matrix-Ungleichungen (LMIs)

\[ \begin{split} \textcolor{red}P &>& 0 \\ A^T\textcolor{red}P+\textcolor{red}PA &<& 0 \end{split} \]

formuliert werden. Gesucht ist also ein positive definite Matrix \(\textcolor{red}P\) welche zusätzlich die Matrix-Ungleichung \(A^T\textcolor{red}P+\textcolor{red}PA < 0\) erfüllt.

Für eine schnelle Wiederholung der Definitheit von Matrizen sei auf Wikipedia: Definitheit von Matrizen. Wir wollen die dortigen Ergebnisse hier kurz wiederholen.

Hinweis

Eine beliebige (ggf. symmetrische bzw. hermitesche) Matrix \(A \in R^{n \times n}\) ist

\[ \begin{split} & \text{positiv definit, } & \text{falls } x^TAx >0 \\ & \text{positiv semidefinit, } & \text{falls } x^TAx \ge 0 \\ & \text{negativ definit, } & \text{falls } x^TAx < 0 \\ & \text{negativ semidefinit, } & \text{falls } x^TAx \le 0 \\ \end{split} \]

für alle \(n\)-zeiligen Spaltenvektoren \(x\in V\) mit \(x\neq 0\), wobei \(x^T\) der Zeilenvektor ist, der aus dem Spaltenvektor \(x\) durch Transponieren hervorgeht.

Für eine Überprüfung sind diese Ergebnisse geeignet:

Tipp

Eine quadratische symmetrische (bzw. hermitesche) Matrix ist genau dann

\[ \begin{split} & \text{positiv definit, } & \text{wenn alle Eigenwerte größer als null sind;} \\ & \text{positiv semidefinit, } & \text{wenn alle Eigenwerte größer oder gleich null sind;} \\ & \text{negativ definit, } & \text{wenn alle Eigenwerte kleiner als null sind;} \\ & \text{negativ semidefinit, } & \text{wenn alle Eigenwerte kleiner oder gleich null sind und} \\ & \text{indefinit, } & \text{wenn positive und negative Eigenwerte existieren.;} \end{split} \]

Beispiel: Gegeben sei ein lineares System:

\[ A = \left[\begin{matrix}0 & 0 & 1 & 0\\0 & 0 & 0 & 1\\- \frac{c_{1} + c_{2}}{m_{1}} & \frac{c_{2}}{m_{1}} & - \frac{d_{1} + d_{2}}{m_{1}} & \frac{d_{2}}{m_{1}}\\\frac{c_{2}}{m_{2}} & \frac{- c_{2} - c_{3}}{m_{2}} & \frac{d_{2}}{m_{2}} & \frac{- d_{2} - d_{3}}{m_{2}}\end{matrix}\right] \]

Wenn die Reibterme \(d_1,d_2,d_3\) größer \(0\) sind, besitzt die Matrix \(A\) nur negative Eigenwerte.

m1 = 1.0
d1 = 0.1
c1 = 1.0

m2 = 1.0
d2 = 0.1
c2 = 1.0

d3 = 0.5
c3 = 1.0
A = np.array([[0., 0., 1., 0.], [0., 0., 0., 1.], [-(c1+c2)/m1, c2/m1, -(d1+d2)/m1, d2/m1], [c2/m2, -(c2+c3)/m2, d2/m2, -(d2+d3)/m2]])
B = np.array([[0., 0.], [0., 0.], [1/m1, 0.], [0., 1/m2]])
C = np.eye(4)
D = np.zeros((4,2))

sys_c = signal.StateSpace(A, B, C, D)
#A = np.matrix('0 1; -1 -2')
np.linalg.eigvals(A) < 0
array([ True,  True,  True,  True])

Dieses System ist somit stabil. Im Folgenden wollen wir die Stabilität mit der Hilfe von LMIs überprüfen.

A = cp.Parameter((4,4))
P = cp.Variable((4,4))

objective = cp.Minimize( 0 )
I = np.identity(4)
prob = cp.Problem(objective, [A.T@P+P@A+0.5*P << 0, P - 1e-10*I >> 0])
#prob = cp.Problem(objective, [A.T*P+P*A << 0, P >> 0])
A.value = np.array([[0., 0., 1., 0.], [0., 0., 0., 1.], [-(c1+c2)/m1, c2/m1, -(d1+d2)/m1, d2/m1], [c2/m2, -(c2+c3)/m2, d2/m2, -(d2+d3)/m2]])
prob.solve()
0.0
print(P.value)
[[ 1.39496667e-10 -1.32630294e-11  7.72824528e-12 -1.97135398e-12]
 [-1.32630294e-11  1.41039950e-10  1.16687253e-12  1.39469830e-11]
 [ 7.72824528e-12  1.16687253e-12  9.69395908e-11  3.32286293e-11]
 [-1.97135398e-12  1.39469830e-11  3.32286293e-11  9.50517968e-11]]
np.linalg.eigvals(P.value) > 0
array([ True,  True,  True,  True])

Wie wir sehen sind alle Eigenwerte größer null.

np.linalg.eigvals((A.T@P+P@A).value) < 0
array([ True,  True, False,  True])

Wie wir sehen sind alle Eigenwerte kleiner null. Das System ist stabil.

Alternative Implementierung:

Weiters ist es möglich zusätzliche Zielfunktion zu den LMIs hinzuzufügen:

TODO Erklärung warum

objective = cp.Minimize( cp.lambda_max(P) )
prob = cp.Problem(objective, [A.T@P+P@A+0.5*P << 0, P - 1e-10*I >> 0])
prob.solve()
1.0924596303692737e-10
print(P.value)
[[ 9.97497860e-11 -8.10039929e-12  4.83061333e-12 -1.08614965e-12]
 [-8.10039929e-12  1.00250168e-10 -5.58004014e-13  8.04459401e-12]
 [ 4.83061333e-12 -5.58004014e-13  7.20952608e-11  2.17222304e-11]
 [-1.08614965e-12  8.04459401e-12  2.17222304e-11  7.04952760e-11]]
np.linalg.eigvals(P.value) > 0
array([ True,  True,  True,  True])

Wie wir sehen sind alle Eigenwerte größer null.

np.linalg.eigvals((A.T@P+P@A).value) < 0
array([ True, False,  True,  True])

Wie wir sehen sind alle Eigenwerte kleiner null. Das System ist stabil.

Zustandsregler

Gegeben sei ein lineares System

\[ \dot{x} = Ax + Bu \]

wo \(x \in \mathbb{R}^n\) und \(u \in \mathbb{R}^m\) der Zustand und Eingangsvektor. Das Ziel ist einen Zustandsregler der Form

\[ u = K x \]

welcher das geschlossen System

\[ \dot{x} = (A+BK)x \]

stabilisiert.

Diese System ist stabil, wenn ein \(P\) existiert:

\[ \begin{split} \textcolor{red}{P} &> 0 \\ (A+B\textcolor{red}{K})^T\textcolor{red}{P}+\textcolor{red}{P}(A+B\textcolor{red}{K}) &< 0 \end{split} \]

Die nicht bekannten Matrizen sind mit ROT. markiert. Wie wir nun leicht erkennen können ist dies keine Lineare Matrix-Ungleichung (LMI) sondern eine bilineare Matrix-Ungleichung (BMI). BMI’s sind deutlich schwerer zu lösen. Es gibt aber einige Möglichkeiten BMI’s in LMI’s umzuformen.

Variante I:

Wir wissen, dass die Eigenwerte einer Matrix auch die Eigenwerte der transponierten Matrix sind. Ein System \(\dot{x} = (A+BK)x\) ist genau dann stabil wenn auch sein duales System

\[ \dot{x} = (A+BK)^Tx \]

stabil ist.

Die Stabilitäts-Ungleichungen lauten für das duale System:

\[ \begin{split} \textcolor{red}Q &> 0 \\ (A+B\textcolor{red}K)\textcolor{red}Q+\textcolor{red}Q(A+B\textcolor{red}K)^T &< 0 \end{split} \]

Die ist noch immer ein BMI. Jedoch, wenn wir eine neue Variable \(Y=KQ\) einführen, lauten die Ungleichungen nun:

\[ \begin{split} \textcolor{red}Q &> 0 \\ A\textcolor{red}Q+\textcolor{red}QA^T+B\textcolor{red}Y+\textcolor{red}Y^TB^T &< 0 \end{split} \]

Dies ist nun ein LMI Problem. Nachdem das LMI Problem gelöst ist, erhalten wir die Reglermatrix:

\[ K = YQ^{-1} \]

Variante II:

Ein anderer Weg die ursprüngliche BMI

\[ \begin{split} \textcolor{red}P &> 0 \\ (A+B\textcolor{red}K)^T\textcolor{red}P+\textcolor{red}P(A+B\textcolor{red}K) &< 0 \end{split} \]

in ein LMI umzuformen ist durch ein beidseitiges multiplizieren von \(P^{-1}\)

\[ \begin{split} \textcolor{red}P^{-1} &> 0 \\ \textcolor{red}P^{-1}(A+B\textcolor{red}K)^T+(A+B\textcolor{red}K)\textcolor{red}P^{-1} &< 0 \end{split} \]

und dem Ersetzen von \(\textcolor{red}Q=\textcolor{red}P^{-1}\)

\[ \begin{split} \textcolor{red}Q &> 0 \\ \textcolor{red}Q(A+B\textcolor{red}K)^T+(A+B\textcolor{red}K)\textcolor{red}Q &< 0 \end{split} \]

Nun kann wieder der Trick \(Y=KQ\) angewendet werden.

Beispiel: Betrachten wir das folgende lineare System

\[ A = \left[\begin{matrix}0 & 0 & 1 & 0\\0 & 0 & 0 & 1\\- \frac{c_{1} + c_{2}}{m_{1}} & \frac{c_{2}}{m_{1}} & - \frac{d_{1} + d_{2}}{m_{1}} & \frac{d_{2}}{m_{1}}\\\frac{c_{2}}{m_{2}} & \frac{- c_{2} - c_{3}}{m_{2}} & \frac{d_{2}}{m_{2}} & \frac{- d_{2} - d_{3}}{m_{2}}\end{matrix}\right] \]

\[ B = \left[\begin{matrix}0 & 0\\0 & 0\\\frac{1}{m_{1}} & 0\\0 & \frac{1}{m_{2}}\end{matrix}\right] \]

m1 = 1.0
d1 = 0.0
c1 = 1.0

m2 = 1.0
d2 = 0.0
c2 = 1.0

d3 = 0.0
c3 = 1.0

A = np.array([[0., 0., 1., 0.], [0., 0., 0., 1.], [-(c1+c2)/m1, c2/m1, -(d1+d2)/m1, d2/m1], [c2/m2, -(c2+c3)/m2, d2/m2, -(d2+d3)/m2]])
eig_values_c = np.linalg.eigvals(A)
eig_values_c
array([4.16333634e-17+1.73205081j, 4.16333634e-17-1.73205081j,
       5.55111512e-17+1.j        , 5.55111512e-17-1.j        ])
np.linalg.eigvals(A) < 0
array([False, False, False, False])

Das System ist nicht stabil.

A = cp.Parameter((4,4))
B = cp.Parameter((4,2))
Q = cp.Variable((4,4))
Y = cp.Variable((2,4))
I = np.identity(4)

objective = cp.Minimize( cp.lambda_max(Q) )
prob = cp.Problem(objective, [Q - 1e-10*I >> 0, A@Q+Q@A.T+B@Y+Y.T@B.T+0.5*Q << 0])
A.value = np.array([[0., 0., 1., 0.], [0., 0., 0., 1.], [-(c1+c2)/m1, c2/m1, -(d1+d2)/m1, d2/m1], [c2/m2, -(c2+c3)/m2, d2/m2, -(d2+d3)/m2]])
B.value = np.array([[0., 0.], [0., 0.], [1/m1, 0.], [0., 1/m2]])
prob.solve()
1.0000082521412092e-10
K = np.dot(Y.value,np.linalg.inv(Q.value))
print(K)
[[ 1.00000177 -1.00000491 -0.47870018 -0.22831267]
 [-1.00000491  1.00000177 -0.22831267 -0.47870018]]
Acl = (A.value+B.value@K)
eig_values_c_cl = np.linalg.eigvals(Acl)
eig_values_c_cl
array([-0.35350643+0.93543377j, -0.35350643-0.93543377j,
       -0.12519376+0.99212895j, -0.12519376-0.99212895j])
np.linalg.eigvals(Acl) < 0
array([ True,  True,  True,  True])

Wie wir sehen sind alle Eigenwerte des geschlossenen Kreises kleiner null. Wir haben einen stabilisierenden Regler entworfen.

plt.figure(figsize=(6,4))
plt.plot(np.real(eig_values_c),np.imag(eig_values_c), 'bx', label="Offener Regelkreis")
plt.plot(np.real(eig_values_c_cl),np.imag(eig_values_c_cl), 'gx', label="Geschlossener Regelkreis")
plt.vlines(0,-5,5, textcolor='red', linewidth=1.0)
plt.axis('equal')
plt.xlim(-5, 5) 
plt.ylim(-5, 5)
plt.legend()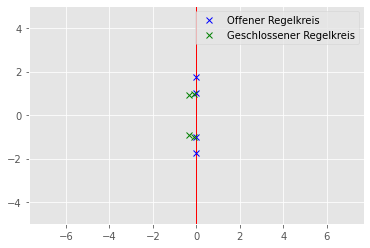

Fazit

LMI’s sind ein wichtiges Werkzeug für die moderne Regelungstechnik. Eine Vielzahl von Problemen in der optimalen und robusten Regelungstheorie lässt sich als LMI’s formulieren und mit Techniken aus der konvexen Optimierungstheorie elegant lösen. Beispielsweise können \(H_2\) und \(H_\infty\) Beobachter- und Reglersynthesen durchgeführt werden.

Referenzen