import numpy as np
from numpy import sin, cos
import control as ctrl
import matplotlib.pyplot as plt
plt.style.use('ggplot')In diesem Notebook wollen wir eine Systemanalyse durchführen wie sie in der Kontrolltheorie üblich ist. Die Python Bibliothek control liefert einen guten Funktionsumfang um eine solche Systemanalyse durchzuführen.
System
Bewegungsgleichung
Gegeben sei wieder die Bewegungsgleichung
\[ \mathbf{M}(\mathbf{q})\ddot{\mathbf{q}} + \mathbf{g}(\mathbf{q},\dot{\mathbf{q}}) = \mathbf{Q}(\mathbf{q}) \]
für das Masse Feder System
\[ \begin{bmatrix} m_1 & 0 \\ 0 & m_2 \end{bmatrix} \begin{bmatrix} \ddot{q}_1 \\ \ddot{q}_2 \end{bmatrix} + \begin{bmatrix} d_{1}\dot{q}_1+d_{2}(\dot{q}_1+\dot{q}_2)+c_{1}q_1+c_{2}(q_1-q_2) \\ d_{3}\dot{q}_2-d_{2}(\dot{q}_1-\dot{q}_2)+c_{3}q_2-c_{2}(q_1-q_2) \end{bmatrix} = \begin{bmatrix} F_{1} \\ F_{2} \end{bmatrix}. \]
Auch im Konfigurationsraum können wir eine Systemanalyse durchführen. Mit den Stabilitätssätzen der Mechanik existieren elegante Sätze für Stabilitätsuntersuchungen.
Zustandsraum
Gängiger ist aber die Systemanalyse in der Zustandsraumdarstellung
\[ \begin{split} \dot{\mathbf{x}} &= \mathbf{A}_c \mathbf{x} + \mathbf{B}_c \mathbf{u} \\ \mathbf{y} &= \mathbf{C}_c \mathbf{x} + \mathbf{D}_c \mathbf{u} \end{split} \]
durchzuführen. Für das Masse-Feder-System lauten diese
\[ \begin{bmatrix} \dot{x}_1 \\ \dot{x}_2 \\ \dot{x}_3 \\ \dot{x}_4 \end{bmatrix} = \begin{bmatrix} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ -\frac{c_1+c_2}{m_1} & \frac{c_2}{m_1} & -\frac{d_1+d_2}{m_1} & \frac{d_1}{m_1} \\ \frac{c_2}{m_2} & -\frac{c_2+c_3}{m_2} & \frac{d_2}{m_2} & -\frac{d_2+d_3}{m_2} \end{bmatrix} + \begin{bmatrix} 0 & 0 \\ 0 & 0 \\ \frac{1}{m_1} & 0 \\ 0 & \frac{1}{m_2} \end{bmatrix} \begin{bmatrix} F_1 \\ F_2 \end{bmatrix}. \]
Für Abtastsystem können wir auch die zeitdiskrete Formulierung
\[ \begin{split} \mathbf{x}_{k+1} &= \mathbf{A}_d \mathbf{x}_k + \mathbf{B}_d \mathbf{u}_k \\ \mathbf{y}_k &= \mathbf{C}_d \mathbf{x}_k + \mathbf{D}_d \mathbf{u}_k \end{split} \]
untersuchen.
Code
m1 = 1.0
d1 = 0.1
c1 = 1.0
m2 = 1.0
d2 = 0.1
c2 = 1.0
d3 = 0.5
c3 = 1.0Systemanalyse - Zeitkontinuierliches System
TODO: Systemanalyse für zeitkontinuierliche Systeme, Definitionen hinzufügen.
System
A = np.array([[0., 0., 1., 0.], [0., 0., 0., 1.], [-(c1+c2)/m1, c2/m1, -(d1+d2)/m1, d2/m1], [c2/m2, -(c2+c3)/m2, d2/m2, -(d2+d3)/m2]])
B = np.array([[0., 0.], [0., 0.], [1/m1, 0.], [0., 1/m2]])
#C = np.eye(4)
#D = np.zeros((4,2))
C = np.array([[1., 0., 0., 0.],[0., 1., 0., 0.]])
D = np.zeros((2,2))
sys_c = ctrl.ss(A, B, C, D)Stabilität
eig_values_c, _ = np.linalg.eig(sys_c.A)
eig_values_carray([-0.24790466+1.69607215j, -0.24790466-1.69607215j,
-0.15209534+0.99896395j, -0.15209534-0.99896395j])eig_values_c < 0array([ True, True, True, True])plt.figure(figsize=(6,4))
plt.plot(np.real(eig_values_c),np.imag(eig_values_c), 'gx', label="Offener Regelkreis")
plt.vlines(0,-5,5, color='red', linewidth=1.0)
plt.axis('equal')
plt.xlim(-5, 5)
plt.ylim(-5, 5)
plt.legend()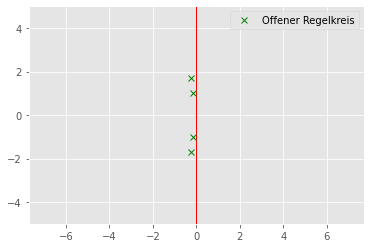
Steuerbarkeit
Oc_c = ctrl.ctrb(sys_c.A,sys_c.B)
np.linalg.matrix_rank(Oc_c)4Beobachtbarkeit
Ob_c = ctrl.obsv(sys_c.A,sys_c.C)
np.linalg.matrix_rank(Ob_c)4Systemanalyse - Zeitdiskretes System
dt = 0.1
sys_d = sys_c.sample(dt, method='zoh')Stablität
Globale asymptotische Stabilität für Abtastsysteme
Das System
\[ x_{k+1} = A_d x_k \]
ist genau dann asymptotisch stabil, wenn alle Eigenwerte der Matrix \(A_d\) im betraglich kleiner als 1 sind.
Man sagt dann auch, die Ruhelage \(x_R = 0\), die der Beziehung \(x_R = A_d x_R\) genügt, ist global asymptotisch stabil.
eig_values_d, _ = np.linalg.eig(sys_d.A)
np.abs(eig_values_d)array([0.97551429, 0.97551429, 0.98490555, 0.98490555])np.abs(eig_values_d) < 1array([ True, True, True, True])plt.figure(figsize=(6,4))
plt.plot(np.real(eig_values_d),np.imag(eig_values_d), 'gx', label="Offener Regelkreis")
draw_circle = plt.Circle((0.0, 0.0), 1.0, color='red', fill=False, linewidth=1.0)
plt.gcf().gca().add_artist(draw_circle)
plt.axis('equal')
plt.xlim(-2, 2)
plt.ylim(-2, 2)
plt.legend()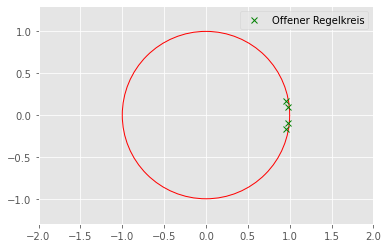
Erreichbarkeit und Steuerbarkeit
Erreichbarkeit:
Der Zustand \(\tilde{x} \in \mathbb{R}^{n}\) des Systems heißt erreichbar, falls eine Folge \((u_k), (k=0,1,\dots,N-1)\) mit \(N < \infty\) existiert, die den Anfangswert \(x_0 = 0\) in den Zustand \(x_N = \tilde{x}\) überführt.
Das System heißt vollständig erreichbar, wenn jeder Zustand \(\tilde{x} \in \mathbb{R}^n\) erreichbar ist.
Erreichbarkeit über die Erreichbarkeitsmatrix
Das System ist genau dann vollständig erreichbar, wenn die sogenannte Erreichbarkeitsmatrix
\[ \mathcal{R}_d = \begin{bmatrix} B_d & A_dB_d & A_d^2B_d & \dots & A_d^{n-1}B_d \end{bmatrix} \]
den Rang \(n\) hat.
Steuerbarkeit:
Der Zustand \(\tilde{x} \in \mathbb{R}^n\) des Systems heißt steuerbar, falls eine Folge \((u_k), k=0,1,\dots,N-1\) mit \(N-1\) mit \(N < \infty\) existiert, die den Anfangswert \(x_0 = \tilde{x}\) in den Zustand \(x_N = 0\) überführt.
Das System heißt vollständig steuerbar, wenn jeder Zustand \(\tilde{x} \in \mathbb{R}^n\) steuerbar ist.
R_d = ctrl.ctrb(sys_d.A,sys_d.B)
np.linalg.matrix_rank(R_d)4Beobachtbarkeit und Rekonstruierbarkeit
Beobachtbarkeit:
Der Zustand \(\tilde{x} \in \mathbb{R}^n\) des Systems heißt beobachtbar, falls eine Folge \((u_k)\) so existiert, daß \(x_0 = \tilde{x}\) aus der Kenntnis der Eingangs- und Ausgangsfolgewerte \(u_k, y_k, (k=0,1,\dots,N)\) ermittelt werden kann.
Das System heißt vollständig beobachtbar, wenn jeder Zustand \(\tilde{x} \in \mathbb{R}^n\) beobachtbar ist.
Beobachtbarkeit über die Beobachtbarkeitsmatrix
Das System ist genau dann vollständig beobachtbar, wenn die sogenannte Beobachtbarkeitsmatrix
\[ \mathcal{O}_d = \begin{bmatrix} C_d \\ C_dA_d \\ C_dA_d^2 \\ \cdots \\ C_dA_d^{n-1} \end{bmatrix} \]
den Rang \(n\) hat.
Rekonstruierbarkeit:
Der Zustand \(\tilde{x} \in \mathbb{R}^n\) des Systems heißt rekonstruierbar, falls eine Folge \((u_k)\) so exisiert, daß \(x_N = \tilde{x}\) aus der Kenntnis der Eingangs- und Ausgangsfolgewerte \(u_k, y_k, (k=0,1,\dots,N)\) ermittelt werden kann.
Das System heißt vollständig rekonstruierbar, wenn jeder Zustand \(\tilde{x}_N \in \mathbb{R}^n\) rekonstruierbar ist.
O_d = ctrl.obsv(sys_d.A,sys_d.C)
np.linalg.matrix_rank(O_d)4Stabilisierbarkeit und Detetkierbarkeit
Stabilisierbarkeit:
Das System heißt stabilisierbar, falls eine Matrix \(K \in \mathbb{R}^{p \times n}\) existiert, so dass die Matrix \(A+BK\) ausschließlich Eigenwerte im Inneren des Einheitskreises besitzt.
Detektierbarkeit:
Das System heißt detektierbar, falls eine Matrix \(\hat{K} \in \mathbb{R}^{p \times q}\) existiert, so daß die Matrix \(A+\hat{K}C\) ausschließlich Eigenwert im Inneren des Einheitskreises besitzt.
Fazit
Ist ein Zustandsraummodell in der zeitkontinuierlichen Form
\[ \begin{split} \dot{\mathbf{x}} &= \mathbf{A}_c \mathbf{x} + \mathbf{B}_c \mathbf{u} \\ \mathbf{y} &= \mathbf{C}_c \mathbf{x} + \mathbf{D}_c \mathbf{u} \end{split} \]
oder in der zeitdiskreten Form
\[ \begin{split} \mathbf{x}_{k+1} &= \mathbf{A}_d \mathbf{x}_k + \mathbf{B}_d \mathbf{u}_k \\ \mathbf{y}_k &= \mathbf{C}_d \mathbf{x}_k + \mathbf{D}_d \mathbf{u}_k \end{split} \]
vorhanden, so können wir diese nutzen um eine Systemanalyse durchzuführen. Mit den gewonnenen Einsichten können wir entscheiden welche Beobachter- und Reglerentwürfe geeignet bzw. möglich sind.
Mathematische Modelle erlauben eine Systemanalyse. Moderne Simulationstools (Modelica, SysML, etc. ) bieten diesen Vorteil oft nicht.