Frequenzkennlinienverfahren (FKL) ~ PI-Regler

Wir haben mit Ziegler-Nichols und Aström-Hägglund schon zwei Tuning-Methoden für den PI-Reglerentwurf kennengelernt. Diese Tuning-Verfahren sind leicht anzuwenden, jedoch haben wir keinerlei Einfluss auf das Ergebnis. Üblicherweise müssen die Regler “per Hand” für den jeweiligen Prozess fein eingestellt werden.

Mit dem Frequenzkennlinienverfahren existiert jedoch eine sehr gute Alternative. Hier können wir unter bestimmten Voraussetzungen Designziele vorgeben, welche auch näherungsweise erreicht werden.

Das Frequenzkennlinenverfahren für PI-Regler ist sehr einfach anzuwenden und sollte in jedem Fall studiert werden. Die Eignung eines PI-Reglers hängt jedoch von den Eigenschaften der Strecke ab und ist somit nicht immer die beste Wahl. Mit dem FKL-Verfahren können aber auch deutlich komplizierte Regler entworfen werden. Dazu sei auf die gängige Literatur verwiesen.

Beispiel

Gegeben sei die Strecke (Rasterkraftmikroskop)

\[ G(s) = \frac{1-e^{-sT_n}}{sT_n(s+1)} \]

wobei für \(T_n = 2n\pi a/\omega_0 = 2n\pi\xi\) gilt. Für dieses Beispiel legen wir die Parameter mit \(\xi=0.002\) und \(n=20\) fest.

Wir wollen nun einen FKL-Entwurf durchführen und das Ergebnis den Tuning-Methoden Ziegler-Nichols und Aström-Hägglund gegenüberstellen. Ziel des Entwurfs wird sein, das Überschwingen zu reduzieren, aber die Anstiegszeit der Tuning-Methoden in etwa zu erreichen.

Der einfache Typ

Der offene Regelkreis (gegebene Strecke + PI-Regler) ist eigentlich nicht vom einfachen Typ. Durch die Pade-Approximation der Totzeit kürzt sich aber im vorliegenden Fall der Integrator und es reicht die Überprüfung der Phasenreserve.

PI-Regler (Tuning)

import numpy as np
import matplotlib.pyplot as plt
plt.style.use('ggplot')

import control as ct

s = ct.tf('s')

n = 20
xi = 0.002 
Tn = 2*n*np.pi*xi

# pade approximation of the delay time
num, den  = ct.pade(Tn,4)
G = ct.minreal((s/s-ct.tf(num,den))/(s*Tn*(s+1)))
G

2 states have been removed from the model

\[\frac{633.3 s^2 + 4.211 \times 10^{5}}{s^5 + 80.58 s^4 + 2929 s^3 + 5.576 \times 10^{4} s^2 + 4.74 \times 10^{5} s + 4.211 \times 10^{5}}\]

def ziegler_nichols(kc,Tc):
    kp = kc*0.45
    #Ti = Tc/1.2
    ki = 0.54*kc/Tc
    return kp, ki

def astrom_hagglund(kc,Tc,K):
    kp = kc*0.16
    ki = (0.16*kc+0.72/K)/(Tc)
    return kp, ki

K = ct.dcgain(G)

gm, pm, wg, wp = ct.margin(G)
kc = gm
wc = wg
Tc = 2*np.pi/wc

kp, ki = ziegler_nichols(kc,Tc)
C_zn = kp+ki/s

kp, ki = astrom_hagglund(kc,Tc,K)
C_ah = kp+ki/s

L_zn = ct.minreal(G*C_zn)
T_zn = ct.feedback(L_zn,1)
L_ah = ct.minreal(G*C_ah)
T_ah = ct.feedback(L_ah,1)

0 states have been removed from the model
0 states have been removed from the model

Die Anstiegszeit wollen wir mit

\[ t_r = \dfrac{1}{s_{max}} \]

abschätzen, wobei die maximale Steigung \(s_{max}\) aus der Impulsantwort ermittelt wird.

plt.figure(figsize=(16,8))
tout, yout = ct.impulse_response(T_zn)
plt.plot(tout, yout, label='Ziegler-Nichols')
slop_zn = np.max(yout)
tout, yout = ct.impulse_response(T_ah)
plt.plot(tout, yout, label='Aström-Hägglund')
slop_ah = np.max(yout)

print("Anstiegszeit:", 1/slop_zn)
print("Anstiegszeit:", 1/slop_ah)

Anstiegszeit: 0.13895359608742808
Anstiegszeit: 0.29460021263087616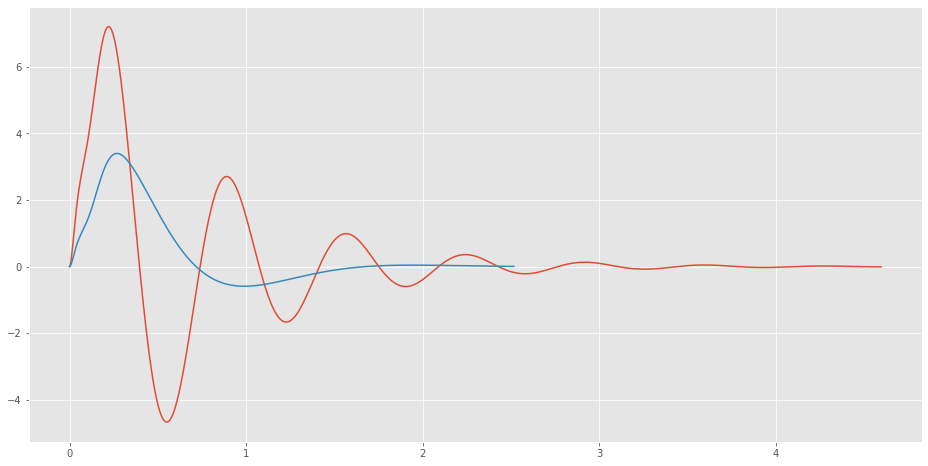

plt.figure(figsize=(16,8))
tout, yout = ct.step_response(T_zn, 10)
plt.plot(tout, yout, label='Ziegler-Nichols')
tout, yout = ct.step_response(T_ah, 10)
plt.plot(tout, yout, label='Aström-Hägglund')
plt.legend()
plt.show()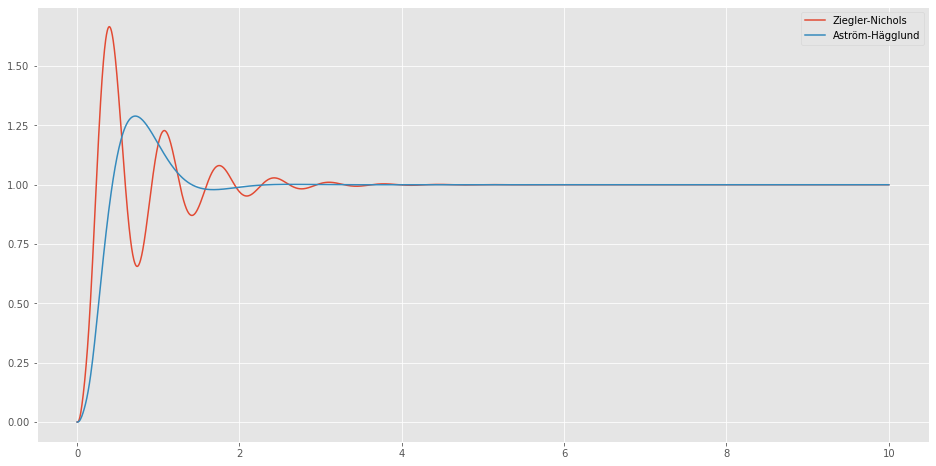

Das Überschwingverhalten vom Ziegler-Nichols ist für viele Prozesse so nicht geeignet. Das Verfahren nach Aström-Hägglund liefert ein deutlich besseres Einschwingverhalten. Jedoch kann auch ein Wert von 25% für das maximale Überschwingen für gewisse Prozesse als zu groß gelten.

PI-Regler (FKL)

Die Struktur des PI-Reglers wird hier mit

\[ C(s) = V_I\frac{(1 + T_Is)}{s} \]

angegeben.

Wir wollen nun die Teile des PI-Reglers analysieren. Der Faktor \(V_I > 0\) hat nur Auswirkung auf den Amplitudengang.

plt.figure(figsize=(16,8))
Vi = 1
Ti = 1
C_V = s/s
_ = ct.bode([C_V],dB=True)
plt.subplot(2,1,1)
plt.ylim([-20,20])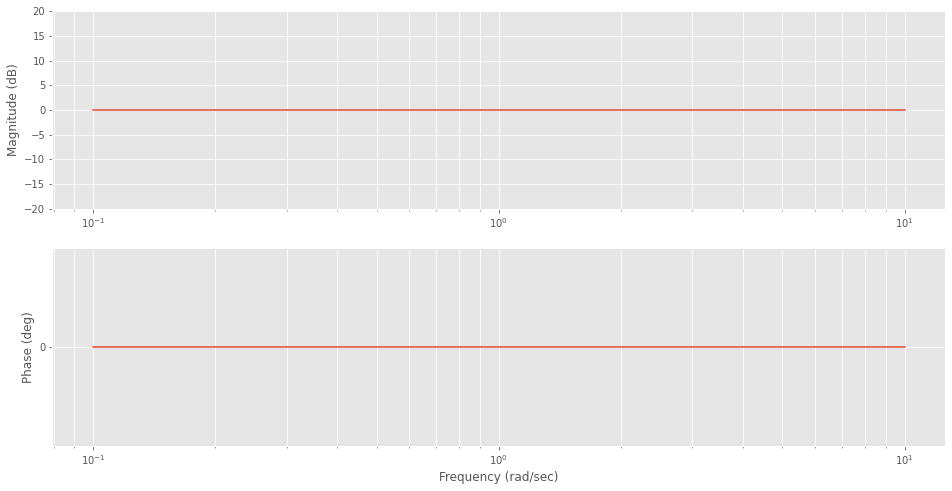

Der Integrator \(\dfrac{1}{s}\) senkt die Phase um \(-90^{\circ}\). Der Amplitudengang wird um 20dB pro Dekade abgesenkt, wobei die 0-dB Linie bei 1 rad/sec durchschritten wird.

plt.figure(figsize=(16,8))
Vi = 1
Ti = 1
C_I = 1/s
_ = ct.bode([C_I], dB=True)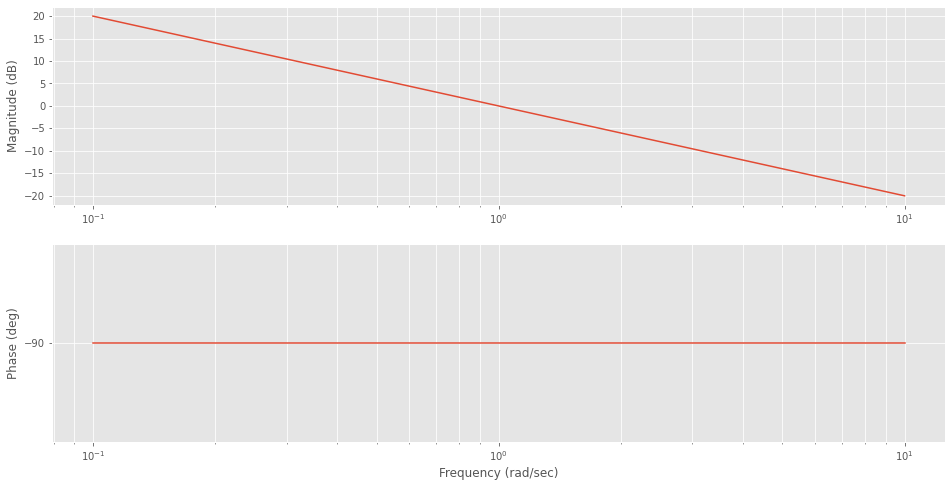

Die Nullstelle \((1 + T_I s)\) hebt den Phasengang um \(90^{\circ}\), wobei bei der Knickfrequenz \(\dfrac{1}{T_i}\) eine Phase von \(45^{\circ}\) erreicht wird. Der Amplitudengang wird näherungsweise bis zu Knickfrequenz nicht beeinflusst, aber ab der Knickfrequenz um 20dB pro Dekade angehoben.

plt.figure(figsize=(16,8))
Vi = 1
Ti = 1
C_T = (1+Ti*s)
_ = ct.bode([C_T], dB=True, wrap_phase=True)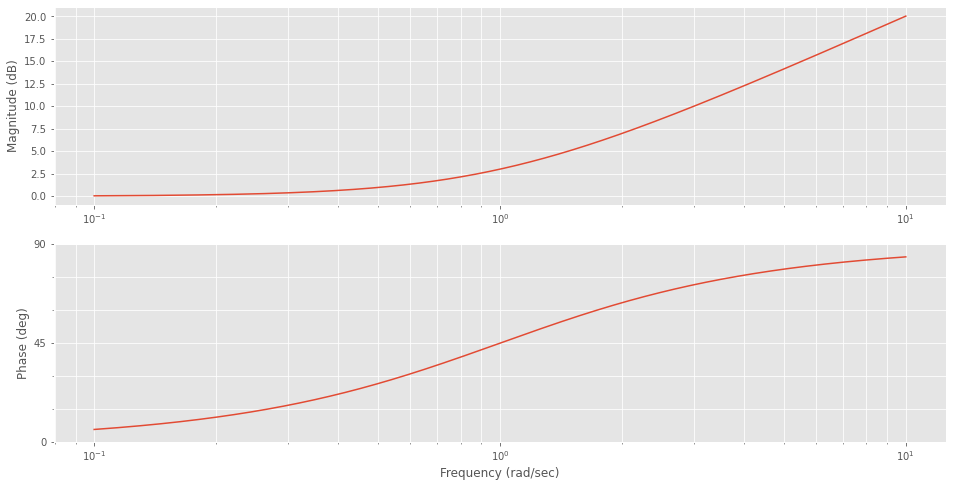

Der PI-Regler senkt also die Phase zwischen \(-90^{\circ}\) und \(0^{\circ}\) ab. Der Amplitudengang fällt bis zur Knickfrequenz um 20dB ab und ist danach konstant.

plt.figure(figsize=(16,8))
Vi = 1
Ti = 1
C1 = Vi*(1+Ti*s)/s

Vi = 10
Ti = 1
C2 = Vi*(1+Ti*s)/s

Vi = 1
Ti = 10
C3 = Vi*(1+Ti*s)/s

_ = ct.bode([C1, C2, C3])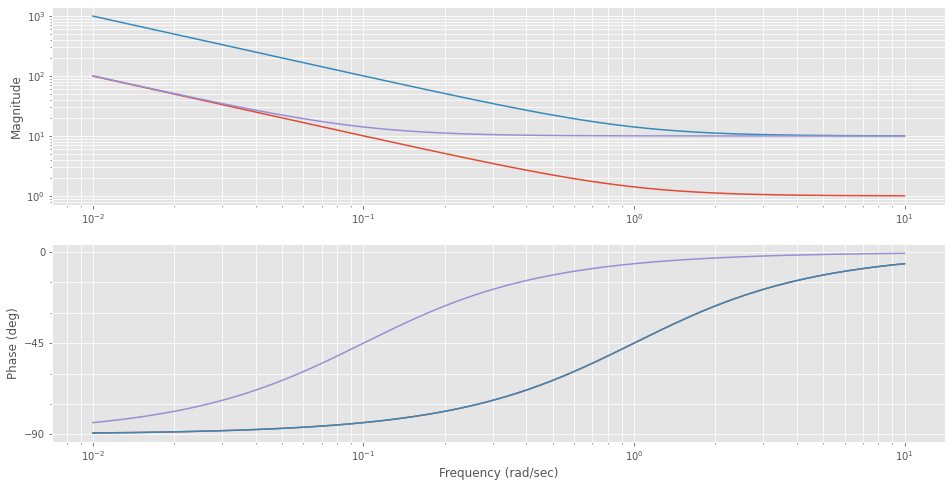

Für den FKL Entwurf wird zuerst die Phase mit dem Term \(\dfrac{(1 + T_I s)}{s}\) angepasst und danach kann der Amplitudengang mit dem Verstärkungsfaktor \(V_I\) wiederum korrigiert werden.

FKL - Entwurf

Im Folgenden ist es unser Ziel, das Überschwingen auf 10% zu beschränken, wobei eine ähnliche Anstiegszeit erreicht werden soll. Die Vorgaben für den geschlossenen Kreis sind also:

Anstiegszeit:

\[ t_r = 0.35 \]

Überschwingen:

\[ ü = 10\% \]

tr = 0.35
wc = 1.5/tr
print(f"Die Durchtrittfrequenz liegt bei {wc = }!")

ue = 10
phi_degree = 70 - ue
print(f"Die Phasenreserve beträgt {phi_degree = }°!")

Die Durchtrittfrequenz liegt bei wc = 4.285714285714286!
Die Phasenreserve beträgt phi_degree = 60°!

plt.figure(figsize=(16,8))
_ = ct.bode(G, dB=True, margins=True, label='P')
plt.subplot(2,1,1)
plt.vlines([wc,wc],ymin=-100,ymax=100, color='black')
plt.subplot(2,1,2)
plt.vlines([wc,wc],ymin=-270,ymax=0, color='black')
plt.legend()
plt.show()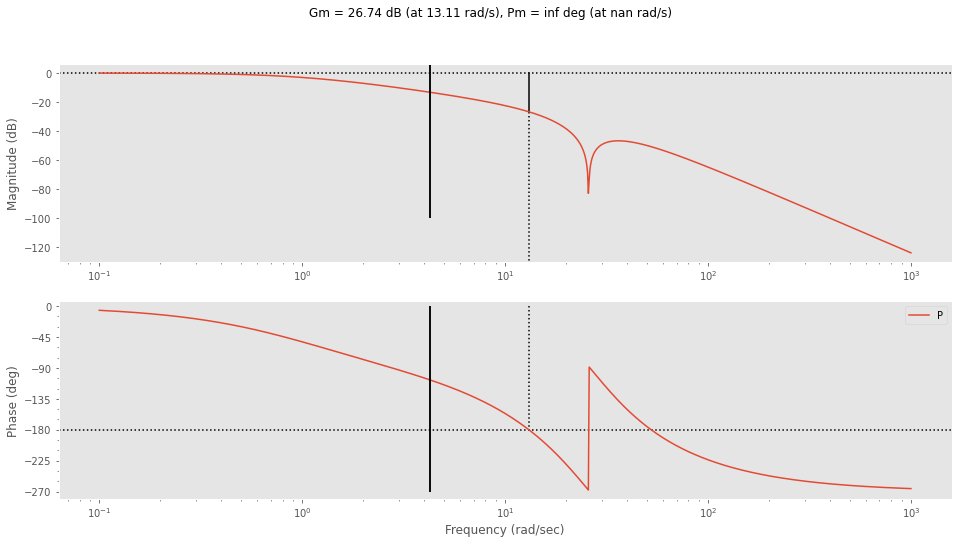

Im ersteren Schritt werden alle bekannten Teile des offenen Kreises multipliziert und mit

\[ L_1 = \frac{1}{s}G(s) \]

bezeichnet. Wir können nun die Phase

\[ \alpha_{act} = \arg{L_1(j\omega_c)} \]

an der Stelle \(\omega_c\) ermitteln und mit dem Sollwert vergleichen. Die Phase muss dann um die Differenz korrigiert werden.

# open loop, known parts
L1 = 1/s*G

# margins
gm, pm, wcg, wcp = ct.margin(L1)

# frequency response data at wc
gc, ac, wc_ = ct.freqresp(L1,wc)

# TODO: cleaner way to do that?
print("arg(L(jw_c)) in rad/sec:",ac[0], "arg(L(jw_c)) in rad/sec:", ac[0]*180/np.pi)
if (ac > 0):
    alpha_act = ac[0] -2*np.pi
else:
    alpha_act = ac[0]
print("arg(L(jw_c)) in rad/sec:", alpha_act, "arg(L(jw_c)) in rad/sec:", alpha_act*180/np.pi)

arg(L(jw_c)) in rad/sec: 2.8322658833800807 arg(L(jw_c)) in rad/sec: 162.27688157657045
arg(L(jw_c)) in rad/sec: -3.4509194237995056 arg(L(jw_c)) in rad/sec: -197.72311842342958

plt.figure(figsize=(16,8))
_ = ct.bode(G, dB=True, label='G')
_ = ct.bode(L1, dB=True, label='L1', margins=True)
plt.subplot(2,1,1)
plt.vlines([wc,wc],ymin=-100,ymax=100, color='black')
plt.subplot(2,1,2)
plt.vlines([wc,wc],ymin=-270,ymax=0, color='black')
plt.legend()
plt.show()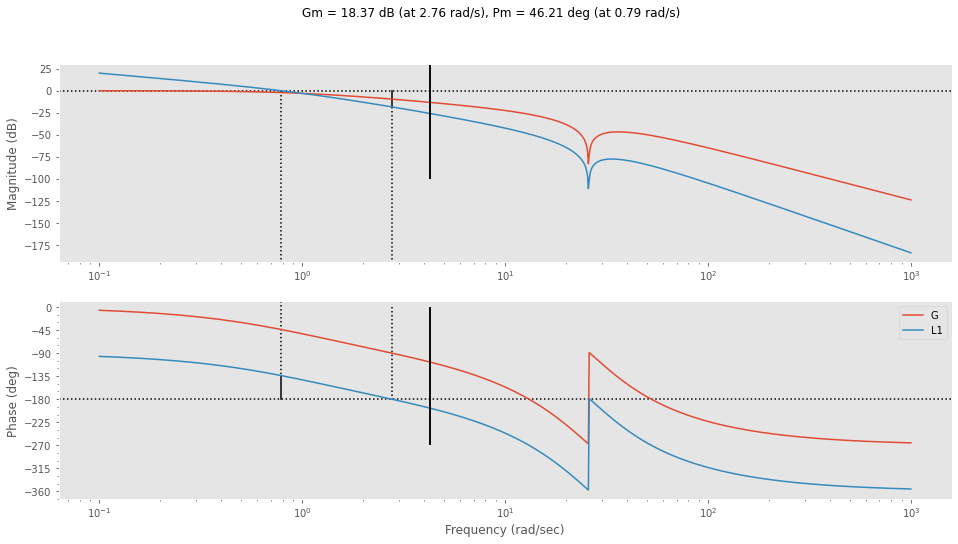

Die Phasendifferenz können wir mit

\[ \Delta \varphi = \alpha_{set} - \alpha_{act} = (\phi_m - 180^{\circ}) - \arg(L_1(j\omega_c)) \]

berechnen. Diese Phasendifferenz wollen wir mit

\[ \arg(1 + j \omega_c T_I) = \arctan \left( \frac{\Im(1 + j \omega_c T_I)}{\Re(1 + j \omega_c T_I)} \right) = \arctan(\omega_c T_I) = \Delta \varphi \]

beseitigen. Daraus können wir den Faktor

\[ T_I = \dfrac{1}{\omega_c} \tan(\Delta \varphi) \]

berechnen.

# set phase at wc
alpha_set_degree = phi_degree - 180
print("Soll Phase bei wc: ", alpha_set_degree)

# delta phase at wc
delta_phi_degree = alpha_set_degree - alpha_act*180/np.pi
delta_phi = delta_phi_degree*np.pi/180
print("Anheben der Phase um: ", delta_phi_degree)

Soll Phase bei wc:  -120
Anheben der Phase um:  77.72311842342958

Ti = 1/wc*np.tan(delta_phi)
print(f"{Ti = }")

# sanity check, delta phi
ct.freqresp((1+Ti*s),wc)[1][0]*180/np.pi

Ti = 1.0722417197380072

77.72311842342958

Nun werden alle bisher bekannten Teile des offenen Kreises mit

\[ L_2(s) = \dfrac{1 + sT_I}{s} G(s) \]

bezeichnen. Die Verstärkung \(V_I\) soll so angepasst werden, dass für den offenen Kreis an der Stelle \(\omega_c\)

\[ |L(j \omega_c)| = V_I |L_2(j \omega_c)| = 1 \]

gilt. Den Verstärkungsfaktor können wir nun mit

\[ V_I = \dfrac{1}{|L_2(j \omega_c)|} \]

berechnen. Der Entwurf ist hiermit abgeschlossen.

L2 = (1+Ti*s)/s*G
gain_correction = ct.freqresp(L2,wc)[0][0]
print("Verstärkung bei wc: ", gain_correction)

Vi = 1/gain_correction
print("Die Verstärkung: ", Vi)

Verstärkung bei wc:  0.23746719603817032
Die Verstärkung:  4.2111079622099075

# sanity check, open loop gain & phase at wc
C = Vi*(1+Ti*s)/s
L = ct.minreal(G*C)
print("Verstärkung bei wc: ", ct.freqresp(L,wc)[0][0])
print("Phase bei wc", ct.freqresp(L,wc)[1][0]*180/np.pi)

0 states have been removed from the model
Verstärkung bei wc:  0.9999999999999999
Phase bei wc -119.99999999999999

omega_limits = [1e-1,1e2]
plt.figure(figsize=(16,8))
_ = ct.bode(G, dB=True, omega_limits=omega_limits, label='G')
_ = ct.bode(L1, dB=True, omega_limits=omega_limits, label='L1')
_ = ct.bode(L, dB=True, omega_limits=omega_limits, label='L', margins=True)
plt.subplot(2,1,1)
plt.legend()
plt.show()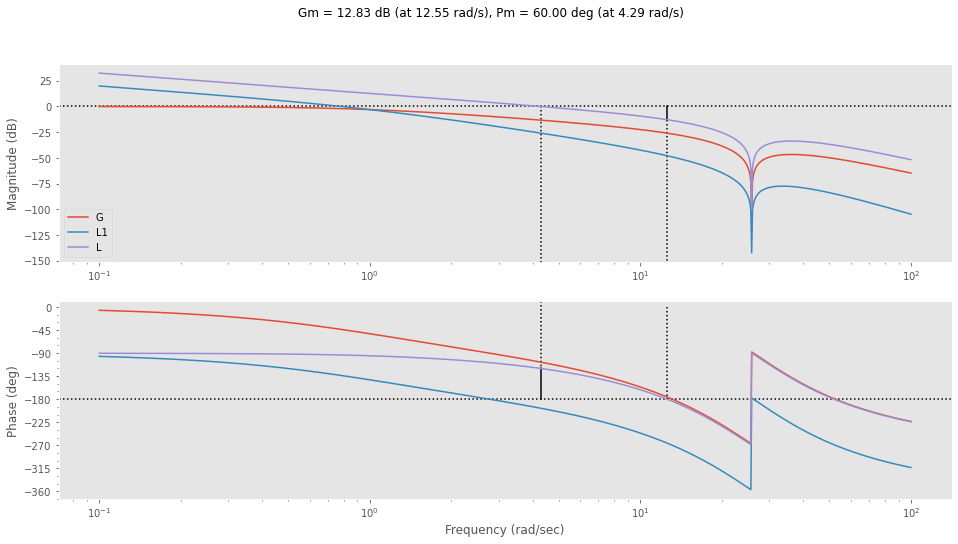

\[\frac{4.515 s + 4.211}{s}\]

\[\frac{2859 s^3 + 2667 s^2 + 1.901 \times 10^{6} s + 1.773 \times 10^{6}}{s^6 + 80.58 s^5 + 2929 s^4 + 5.576 \times 10^{4} s^3 + 4.74 \times 10^{5} s^2 + 4.211 \times 10^{5} s}\]

T = ct.minreal(L/(1+L))
T

6 states have been removed from the model

\[\frac{2859 s^3 + 2667 s^2 + 1.901 \times 10^{6} s + 1.773 \times 10^{6}}{s^6 + 80.58 s^5 + 2929 s^4 + 5.862 \times 10^{4} s^3 + 4.766 \times 10^{5} s^2 + 2.322 \times 10^{6} s + 1.773 \times 10^{6}}\]

omega_limits = [1e-1,1e3]
plt.figure(figsize=(16,8))
_ = ct.bode(G, dB=True, omega_limits = omega_limits, label='G')
_ = ct.bode(T, dB=True, omega_limits = omega_limits, label='T')
plt.subplot(2,1,1)
plt.legend()
plt.show()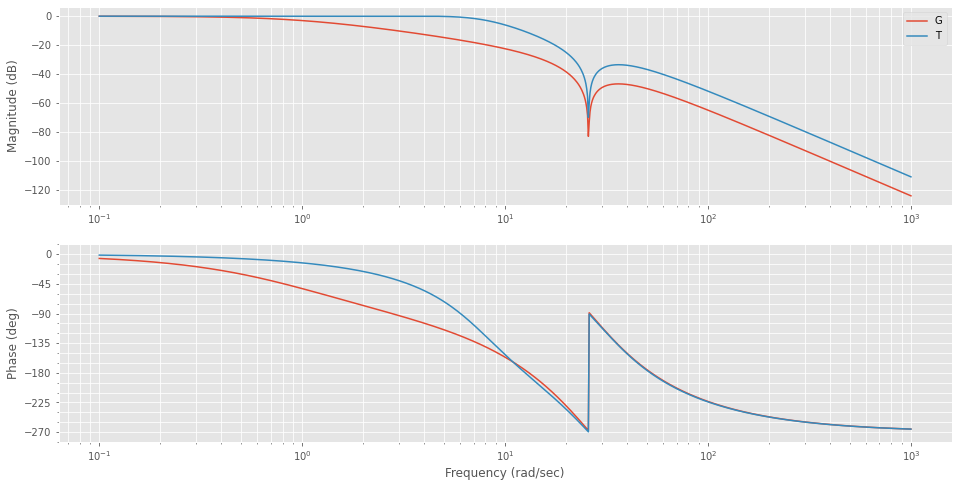

Vergleich der Regler

Die Stabilität und Robustheit lässt sich anhand der Stabilitätsreserven überprüfen.

Die Stabilitätsreserven (stability-margins) bestehen aus

der Amplitudenreserve (gain-margin)
der Phasenrserve (phase-margin)
der Stabilitätsreserve (stability-margin)

Eine weitere Reserve wäre mit der Verzögerungsreserve (delay-margin) gegeben. Diese wollen wir hier nicht weiter betrachten.

# ziegler-nichols
gm, pm, sm, wpc, wgc, wms = ct.stability_margins(L_zn)
print(f"{gm = :.2f} {pm = :.2f} {sm = :.2f}")
# aström-hägglund
gm, pm, sm, wpc, wgc, wms = ct.stability_margins(L_ah)
print(f"{gm = :.2f} {pm = :.2f} {sm = :.2f}")
# fkl
gm, pm, sm, wpc, wgc, wms = ct.stability_margins(L)
print(f"{gm = :.2f} {pm = :.2f} {sm = :.2f}")

gm = 1.68 pm = 19.91 sm = 0.27
gm = 4.71 pm = 43.60 sm = 0.61
gm = 4.38 pm = 60.00 sm = 0.65

Die Methode nach Ziegler-Nichols liefert die geringsten Stabilitätsreserven, und der Regler hat somit schlechte Robustheit-Eigenschaften und zeigt ein aggressives Ausregelverhalten. Die Methoden Aström-Hägglund und FKL haben ähnliche Reserven bezüglich der Amplitude (\(G_M\)) als auch der Stabilität (\(S_M\)). Jedoch liefert das FKL-Verfahren eine deutlich größere Phasenreserve (\(P_M\)), was zu einem geringeren Überschwingen führt.

Für die visuelle Überprüfung der Stabilitätsreserven können wir das Nyquist-Diagramm zeichnen. Die deutlichen Unterschiede bezüglich der Phasenreserve ist hier sehr gut zu erkennen.

plt.figure(figsize=(16,8))
ct.nyquist([G,L_zn,L_ah, L])
circle1 = plt.Circle((0, 0), 1., color='black', fill=False)
plt.gca().add_patch(circle1)
plt.ylim([-3,3])
plt.xlim([-3,3])
plt.gca().set_aspect('equal', 'box')

# for legend
lines = plt.gca().get_lines()
legend = plt.legend([lines[i] for i in [0,3,6,9]], ["Prozess", "Ziegler-Nichols", "Aström-Hägglund", "FKL"], loc=1)
plt.gca().add_artist(legend)

plt.show()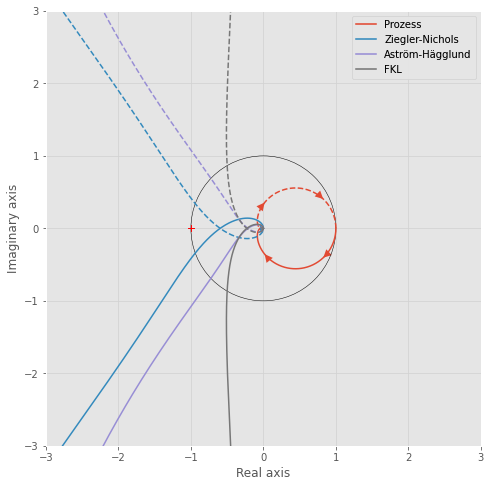

Die Einhaltung der Spezifikation wird durch eine Sprungantwort verifiziert.

tout, yout = ct.impulse_response(T)
slop = np.max(yout)
#plt.plot(tout, yout, label='FKL')
#plt.show()

plt.figure(figsize=(16,8))
tout, yout = ct.step_response(T_zn, 10)
plt.plot(tout, yout, label='Ziegler-Nichols')
tout, yout = ct.step_response(T_ah, 10)
plt.plot(tout, yout, label='Aström-Hägglund')
tout, yout = ct.step_response(T, 10)
plt.plot(tout, yout, label='FKL')
plt.legend()
plt.show()

print("Anstiegszeit in sec (SOLL): ",tr)
print("Anstiegszeit in sec  (IST): ",1/slop)

print("Überschwingen in % (SOLL): ",ue)
print("Überschwingen in %  (IST): ",(np.max(yout)-1)*100)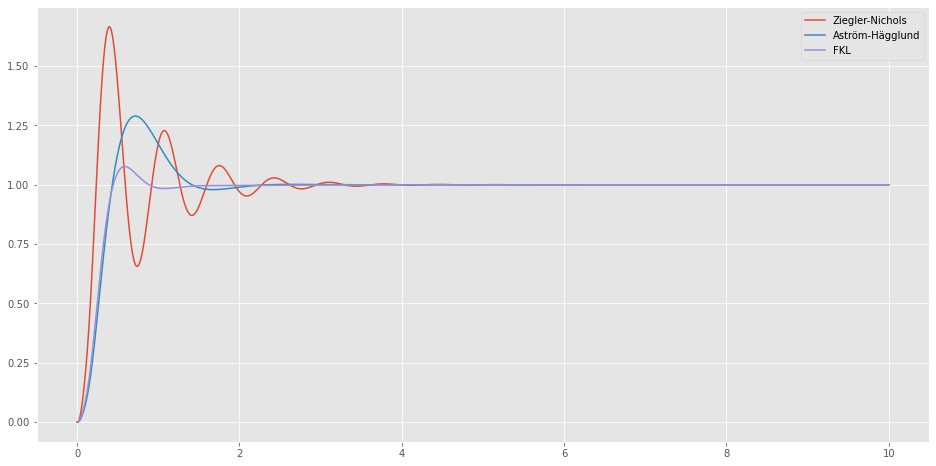

Anstiegszeit in sec (SOLL):  0.35
Anstiegszeit in sec  (IST):  0.28535975053771573
Überschwingen in % (SOLL):  10
Überschwingen in %  (IST):  7.691855734483322

Wir sehen also, dass die Vorgaben für den geschlossenen Regelkreis gut eingehalten werden.

Fazit

Der FKL-Entwurf erlaubt es, das Überschwingverhalten deutlich zu reduzieren. Ein gutes Modell der Strecke ist die Voraussetzung, um das FKL-Verfahren anwenden zu können. Auch ist der Aufwand etwas größer als bei den PID-Faustformeln, jedoch können Eigenheiten der Strecke deutlich besser berücksichtigt werden. Es existieren einige weitere übliche FKL-Entwürfe, zum Beispiel Lead-Lag-Entwurf, Kompensationsentwurf oder Notch-Filter-Entwurf. Mit etwas Übung und vorhandenen Beispielen als Vorlagen können diese Entwürfe sehr gut und schnell mit Python-Control umgesetzt werden.

Referenzen

Feedback Systems: An Introduction for Scientists and Engineers, Second Edition, 2020/2022 (Karl J. Aström, Richard M. Murray)
Automatisierungstechnik 2, WS 2019/2020 REGPRO / JKU (Kurt Schlacher)
Automatisierung, 2021/2022 ACIN / TU WIEN (Andreas Kugi)