Exakte Regler-Gradient Methoden für LQR

Aufbauend auf den letzten Blogeintrag wollen wir hier Regler-Gradient (policy gradient) Methoden besprechen. policy gradient-Methoden können der Regler-Suche / Optimierung (policy search aka policy optimization) zugeordnet werden.

Dieser Blogeintrag basiert sehr stark auf den Ergebnissen, welche im wissenschaftlichen Aufsatz Global Convergence of Policy Gradient Methods for the Linear Quadratic Regulator erarbeitet wurden. Wir wollen diesen Aufsatz mit [Fazel et al., 2018] referenzieren.

Tipp

Im bestärkenden Lernen werden unter policy gradient Methoden meist modellfreie Algorithmen verstanden, welche auf den sogenannten Reinforce oder log derivative-Trick basieren:

Für die Ableitung des Logarithmus gilt

\[ \frac{d}{dx} ln f(x) = \frac{1}{f(x)} \frac{df(x)}{dx}. \]

Dieser Zusammenhang wird für die Herleitung der vanilla policy gradient Methode im bestärkenden Lernen benutzt. Siehe dazu die Herleitung in OpenAI: spinning up - policy optimization.

Im Sinne der Kybernetik fassen wir aber unter policy gradient alle Methoden zusammen, welche das optimale Regelungsproblem mit einem Gradientenabstieg lösen. Der Gradient kann dabei exakt/modellbasiert oder geschätzt/modellfrei sein.

Exkate Regler-Gradienten Methoden

Gegeben sei ein LQR Problem, wobei wir jedoch die Regelstruktur mit \(u_k=-Kx_k\) vorgeben ist. Zusätzlich sei für den Anfangszustand \(x_0\) eine Gauß-Verteilung \(\mathbb{N}(0,\Sigma_0)\) angenommen. Nun lautet das LQR Problem:

\[ \underset{K}{\min} \mathbb{E} \left( \sum_{k=0}^{\infty} {x_k^TQx_k + u_k^TRu_k} \right) \]

\[ \begin{split} \text{subject to} \quad & x_{k+1} = A x_k + B u_k \\ & u = -K x_k \\ & x_0 \sim \mathbb{N}(0,\Sigma_0) \end{split} \]

Die Gesamtkostenfunktion kann in Abhängigkeit des Reglers \(K\) mit

\[ C(K) = \mathbb{E}_{x_0 \sim \mathcal{D}} \left[ \sum_{k=0}^{\infty} x_k^TQ^Tx_k + u_k^{T}Ru_k \right] = \mathbb{E}_{x_0 \sim \mathcal{D}} \left[ \sum_{k=0}^{\infty} x_k^T (Q^T + K^TRK) x_k \right] \]

angegeben werden.

Der Gradientenabstieg aktualisiert den Regler gemäß der Aktualisierungsregel

\[ K \leftarrow K -\eta \nabla C(K). \]

wobei \(\nabla C(K)\) die Ableitung der Kosten bezüglich des Reglers darstellt. Wir können den Gradienten deutlicher in seiner funktionalen Form schreiben. Mit \(P_K\) als Lösung der Lyapunov-Gleichung (Bellman-Gleichung)

\[ P_K = (A - BK)^TP_K(A - BK) + Q + K^TRK \]

lassen sich die totalen Kosten mit

\[ C(K) = \mathbb{E}_{x_0 \sim \mathcal{D}} x_0^T P_K x_0 \]

angeben.

Definieren wir außerdem, \(\Sigma_K\) als die Korrelationsmatrix des Zustands

\[ \Sigma_K = \mathbb{E}_{x_0 \sim \mathcal{D}} \sum_{k=0}^{\infty} x_k x_k^T = \sum_{k=0}^{\infty}(A-BK)^{k}\Sigma_0((A-BK)^T)^{k} \]

ergibt sich die Ableitung zu

\[ \nabla C(K) = 2((R+B^TP_KB)K - B^TP_KA)\Sigma_K. \]

Exakte Regler-Gradient Methode

Gegeben sei

\[ A,B,Q,R,K,\Sigma_0 \]

Löse die Lyapunov-Gleichungen

\[ P_K = (A-BK)^TP_K(A-BK) + Q + K^TRK \]

\[ \Sigma_K = (A-BK)^T\Sigma_K(A-BK) + \Sigma_0 \]

Berechne den Regler-Gradient

\[ E_K = ((R+B^TP_KB)K - B^TP_KA) \]

\[ \nabla C(K) = 2E_K\Sigma_K \]

Aktualisiere den Regler

\[ K \leftarrow K - \eta \nabla C(K) \]

Für dieses Ergebnis gibt es innerhalb der Kontrolltheorie verschiedene Beweise. Wir halten uns aber wieder an das Paper [Fazel et al., 2018].

Beweis:

\[ \begin{split} C_K(x_0) &= x_0^T P_K x_0 \\ &= x_0^T (Q + K^TRK) x_0 + x_0^T (A - BK)^TP_K(A - BK) x_0 \\ &= x_0^T (Q + K^TRK) x_0 + C_K((A - BK)x_0). \end{split} \]

Bezeichnen wir mit \(\nabla\) den Gradienten in Bezug auf \(K\), so ist zu beachten, das \(\nabla C_{\color{red}{K}}((A - BK)x_0)\) zwei Terme hat (einen in Bezug auf im Index \(C_{\color{red}{K}}\) und einen in Bezug auf die Eingabe \((A - BK)x_0\)), dies impliziert

\[ \begin{split} \nabla C_K (x_0) &= 2RKx_0x_0^T - 2B^TP_K(A-BK)x_0x_0^T + \nabla C_K(x_1)|_{x_1 = (A-BK)x_0} \\ &= 2\left((R +B^TP_KB)K - B^TP_KA \right) \sum_{k=0}^{\infty}x_kx_k^T \end{split} \]

wobei die Rekursion und die Beziehung \(x_1 = (A - BK)x_0\) genutzt wurden. Mit der Anwendung des Erwartungswert ist der Beweis erbracht.

Modellbasierte Optimierung: Exakte Gradienten Methoden

In [Fazel et al., 2018], werden drei exakte Aktualisierungsregel angegeben. Für den Regler-Gradientenabstieg (policy gradient descent) lautet die Aktualisierung

\[ K_{n+1} = K_n - \eta \nabla C(K_n). \]

Für den natürlichen Regler-Gradientenabstieg (natural policy gradient descent) wird die Richtung so definiert, dass sie mit dem stochastischen Fall übereinstimmt. Im exakten Fall ist die Aktualisierung

\[ K_{n+1} = K_n - \eta \nabla C(K_n) \Sigma_{K_n}^{-1}. \]

Bei der Gauß-Newton-Methode lautet die Aktualisierung

\[ K_{n+1} = K_{n} - \eta (R + B^TP_{K_n}B)^{-1} \nabla C(K_n) \Sigma_{K_n}^{-1}. \]

Verbindung zur Regler Iteration

Die offline modellbasierte Regleriteration erweist sich als Spezialfall des Gauß-Netwon-Methode, wenn \(\eta = 1\). Durch das einfache Einsetzen kann dies gezeigt werden:

\[ \begin{split} K_{n+1} &= K_{n} - \eta (R + B^TP_{K_n}B)^{-1} \nabla C(K_n) \Sigma_{K_n}^{-1} \\ &= K_{n} - 1 (R + B^TP_{K_n}B)^{-1} E_{K_n} \\ &= K_{n} - 1 (R + B^TP_{K_n}B)^{-1} ((R+B^TP_{K_n}B)K - B^TP_{K_n}A) \\ &= \underset{=0}{\underbrace{\left(I - (R + B^TP_{K_n}B)^{-1} (R+B^TP_{K_n}B) \right)}}K_n + (R + B^TP_{K_n}B)^{-1} B^TP_{K_n}A \\ &= (R + B^TP_{K_n}B)^{-1} B^TP_{K_n}A \end{split} \]

In einem anderen Blogpost wurde die offline modellbasierte Regleriteration schon gezeigt.

Die Gauß-Newton Methode bietet die größte Konvergenzgeschwindigkeit, die Regler-Gradienten Methode besitzt die geringste Konvergenzgeschwindigkeit und die natürliche Regler-Gradienten Methode liegt dazwischen.

Wir können alle drei Methoden in einer Beschreibung angeben.

Exkte Regler-Gradient Methoden

Gegeben sei

\[ A,B,Q,R,K,\Sigma_0 \]

Löse die Lyapunov-Gleichung

\[ P_K = (A-BK)^TP_K(A-BK) + Q + K^TRK \]

\[ \Sigma_K = (A-BK)^T\Sigma_K(A-BK) + \Sigma_0 \]

Regler-Gradient

\[ E_K = ((R+B^TP_KB)K - B^TP_KA) \]

\[ \nabla C(K) = 2E_K \Sigma_K \]

Regler-Aktualisierung

policy gradient

\[ \begin{split} K & \leftarrow K - \eta \nabla C(K) \\ & \leftarrow K - \eta 2 E_K \Sigma_K \end{split} \]

natural policy gradient

\[ \begin{split} K & \leftarrow K - \eta \nabla C(K) \Sigma_{K}^{-1} \\ & \leftarrow K - \eta 2 E_K \end{split} \]

Gauß-Newton

\[ \begin{split} K & \leftarrow K - \eta (R + B^TP_{K}B)^{-1} \nabla C(K) \Sigma_{K}^{-1} \\ & \leftarrow K - \eta (R + B^TP_{K}B)^{-1} E_K \end{split} \]

Modellfreie Optimierung: Geschätzte Gradienten Methoden

In der modellfreien Situation, hat der Regler nur Zugang zu Daten, aber keinen Zugang zu einem Modell. D.h. die Modellparameter \(A,B,Q,R\) sind unbekannt. In der Kontrolltheorie würden wir hier oft eine Systemidentifikation durchführen und dann die Schätzwerte \(\hat{A},\hat{B},\hat{Q},\hat{R}\) in die Riccati-Gleichung einsetzen.

Alternativ können wir aber auch modellfreie Methoden herleiten. In [Fazel et al., 2018] werden zwei modellfreie Methoden (policy gradient und natrual policy gradient) angegeben.

Modellfreie Regler-Gradient Methoden

1: Eingabe \(\rightarrow\) Regler K, Anzahl der Trajektorien m, Länge des Ausrollens l, Glättungsparameter r, Dimension \(d\) (\(x_k \in \mathbb{R}^d\))

2: for \(i,\dots,m\) do

3: \(\qquad\) Ziehen eines Reglers \(\widehat{K}_i = K + U_i\), wobei \(U_i\) gleichmäßig zufällig über Matrizen gezogen wird, deren (Frobenius-)Norm \(r\) ist.

4: \(\qquad\) Simuliere mit \(\widehat{K}_i\) für \(l\) Schritte, gestartet von \(x_o \sim \mathcal{D}\). Dabei sind

\[ \hat{C}_i = \sum_{k=1}^{l} c_k, \quad \hat{\Sigma}_i = \sum_{k=1}^{l} x_kx_k^T \]

empirische Schätzwerte, wobei \(c_k\) und \(x_k\) die Kosten und die Zustände der Trajektorie sind.

5: end for

6: Rückgabe der Schätzungen (biased):

\[ \widehat{C(K)} = \frac{1}{m} \sum_{i = 1}^{m} \frac{d}{r^2} \hat{C}_i U_i \qquad \widehat{\Sigma_K} = \frac{1}{m} \sum_{i=1}^{m} \hat{\Sigma}_i \]

Code

Es werden nur die modellbasierten Methoden implementiert.

import numpy as np
import scipy.signal as signal
import scipy.linalg as linalg
import control as ct
import matplotlib.pyplot as plt
plt.style.use('ggplot')

def dlqr(A,B,Q,R):
    """ solve lqr problem
        returns: controller, value function, closed loop eigenvalues
    """
    
    #first, try to solve the ricatti equation
    P = np.matrix(linalg.solve_discrete_are(A, B, Q, R))
 
    #compute the LQR gain
    K = np.matrix(linalg.inv(B.T@P@B+R)@(B.T@P@A))
 
    eigVals, eigVecs = linalg.eig(A-B@K)
 
    return K, P, eigVals

def policy_evaluation_P(A,B,Q,R,K,S):
    """ policy evaluation via lyapunov equation (bellman equation)
        (A-B K)^T P_K (A-B K) - P_K + Q + K^TRK = 0
        returns: total cost, value functions (matrix)
    """
    
    Ac = A-B@K
    Qc = Q+K.T@R@K
    
    P_K = linalg.solve_discrete_lyapunov(Ac.T,Qc)
    
    C_K = np.trace(P_K@S)
    
    return C_K, P_K

def policy_evaluation_S(A,B,Q,R,K,S):
    """ policy evaluation via lyapunov equation (state correlation matrix)
        (A-B K) S_K (A-B K)^T - S_K + S_0 = 0
        returns: total cost, state correlation matrix
    """
    
    Ac = A-B@K
    
    S_K = linalg.solve_discrete_lyapunov(Ac,S)
    
    C_K = np.trace((Q+K.T@R@K)@S_K)
    
    return C_K, S_K

def gradient_descent(A,B,Q,R,K,Sigma_0):
    """ exact gradient descent
        returns: gradient, total_cost
    """
    
    C_K, P_K = policy_evaluation_P(A,B,Q,R,K,Sigma_0)
    _, Sigma_K = policy_evaluation_S(A,B,Q,R,K,Sigma_0)
    E_K = ((R+B.T@P_K@B)@K-B.T@P_K@A)
    gradient_C = 2*E_K@Sigma_K
        
    return gradient_C, C_K

def natural_gradient_descent(A,B,Q,R,K,Sigma_0):
    """ exact natural gradient descent
        returns: gradient, total_cost
    """
    
    C_K, P_K = policy_evaluation_P(A,B,Q,R,K,Sigma_0)
    E_K = ((R+B.T@P_K@B)@K-B.T@P_K@A)
    gradient_C = 2*E_K
        
    return gradient_C, C_K

def gauß_newton(A,B,Q,R,K,Sigma_0):
    """ exact gauß newton gradient descent
        returns: gradient, total_cost
    """
    
    C_K, P_K = policy_evaluation_P(A,B,Q,R,K,Sigma_0)
    E_K = ((R+B.T@P_K@B)@K-B.T@P_K@A)
    gradient_C = linalg.inv(R+B.T@P_K@B)*2*E_K
        
    return gradient_C, C_K

def all_methods(A,B,Q,R,K0,Sigma0,N,eta1,eta2,eta3):
    """ solve lqr via policy search (policy gradient, natural policy gradient, Gauß-Newton)
    """
    
    K1_list = []
    K1 = K0.copy()
    K1_list.append(K1)
    C1_list = []
    
    K2_list = []
    K2 = K0.copy()
    K2_list.append(K2)
    C2_list = []
    
    K3_list = []
    K3 = K0.copy()
    K3_list.append(K3)
    C3_list = []
    
    for i in range(N):
        g1_cost, c1_cost = gradient_descent(A,B,Q,R,K1,Sigma0)
        K1 = K1 - eta1*g1_cost
        K1_list.append(K1)
        C1_list.append(c1_cost)
        
        g2_cost, c2_cost = natural_gradient_descent(A,B,Q,R,K2,Sigma0)
        K2 = K2 - eta2*g2_cost
        K2_list.append(K2)
        C2_list.append(c2_cost)
        
        g3_cost, c3_cost = gauß_newton(A,B,Q,R,K3,Sigma0)
        K3 = K3 - eta3*g3_cost
        K3_list.append(K3)
        C3_list.append(c3_cost)
        
    return K1, K1_list, C1_list, K2, K2_list, C2_list, K3, K3_list, C3_list

Wir wollen ein System mit praktischer Relevanz verwenden. Dazu definieren wir ein Masse-Feder-Dämpfer System mit einer Kraft als Eingang.

m1 = 10

d1 = 0.01
c1 = 0.5

d2 = 0.01
c2 = 0.5

Ac = np.array([[0, 1.],[-(c1+c2)/m1, -(d1+d2)/m1]])
Bc = np.array([[0.], [1./m1]])
Cc = np.eye(2)
Dc = np.zeros((2,1))

sys_c = signal.StateSpace(Ac, Bc, Cc, Dc)
dt = 0.1
sys_d = sys_c.to_discrete(dt)
A = sys_d.A.astype(np.float128)
B = sys_d.B.astype(np.float128)

Da das System durch die gewählte Dämpfung stabil ist, können wir einfach \(K_0 = 0\) als initialen Regler verwenden.

K0 = np.zeros((1,2)).astype(np.float128)

n, p = B.shape
Q = np.eye(n).astype(np.float128)*10
R = np.eye(p).astype(np.float128)*5
Sigma_0 = np.array([[1. ,.5],[.5, 1.]]).astype(np.float128)*1

Für jedes der drei Verfahren müssen geeignete Lernraten gefunden werden, so dass der Regler zum optimalen Wert konvergiert. Für zu große Lernraten konvergieren die Verfahren nicht.

N = 500
eta1 = np.array([1e-7]).astype(np.float128)
eta2 = np.array([1e-2]).astype(np.float128)
eta3 = np.array([5e-1]).astype(np.float128)

K_infinite, P_infinite, eigVals_closed = dlqr(A,B,Q,R)
C_infinite, _ = policy_evaluation_P(A,B,Q,R,K_infinite,Sigma_0)
K_infinite

matrix([[0.69725191, 4.01299517]], dtype=float128)

K1, K1_list, C1_list, K2, K2_list, C2_list, K3, K3_list, C3_list = all_method(A,B,Q,R,K0,Sigma_0,N,eta1,eta2,eta3)

K1_array = np.array(K1_list).squeeze()
K2_array = np.array(K2_list).squeeze()
K3_array = np.array(K3_list).squeeze()

K1_delta_norm = np.zeros(K1_array.shape[0])
K2_delta_norm = np.zeros(K2_array.shape[0])
K3_delta_norm = np.zeros(K3_array.shape[0])

C1_array = np.array(C1_list).squeeze()
C2_array = np.array(C2_list).squeeze()
C3_array = np.array(C3_list).squeeze()

C1_delta_norm = np.zeros(C1_array.shape[0])
C2_delta_norm = np.zeros(C2_array.shape[0])
C3_delta_norm = np.zeros(C3_array.shape[0])

for i in range(0,K1_array.shape[0]):
    K1_delta_norm[i] = np.linalg.norm(K1_array[i] - K_infinite)/np.linalg.norm(K_infinite)
    K2_delta_norm[i] = np.linalg.norm(K2_array[i] - K_infinite)/np.linalg.norm(K_infinite)
    K3_delta_norm[i] = np.linalg.norm(K3_array[i] - K_infinite)/np.linalg.norm(K_infinite)

for i in range(0,C1_array.shape[0]):
    C1_delta_norm[i] = (C1_array[i] - C_infinite)/C_infinite
    C2_delta_norm[i] = (C2_array[i] - C_infinite)/C_infinite
    C3_delta_norm[i] = (C3_array[i] - C_infinite)/C_infinite

print(K_infinite, "K^* via riccati: ")
print(K1, "K via gradient descent: ")
print(K2, "K via natural gradient descent: ")
print(K3, "K via Gauß-Newton: ")

[[0.69725191 4.01299517]] K^* via riccati: 
[[0.10912518 1.61390732]] K via gradient descent: 
[[0.69725191 4.01299517]] K via natural gradient descent: 
[[0.69725191 4.01299517]] K via Gauß-Newton:

plt.plot(K1_delta_norm,'red',label='gradient descent')
plt.plot(K2_delta_norm,'blue',label='natural gradient descent')
plt.plot(K3_delta_norm,'green',label='Gauß-Newton')
plt.legend()
plt.xlabel('iteration')
plt.ylabel(r'$\frac{\left\Vert K-K* \right\Vert}{\left\Vert K* \right\Vert}$',usetex=True)
#plt.yscale('log')
plt.show()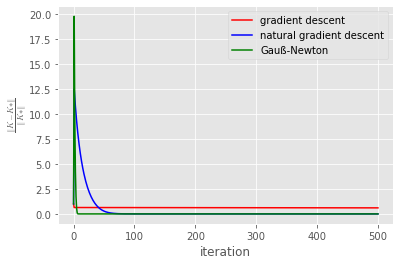

plt.plot(C1_delta_norm,'red',label='gradient descent')
plt.plot(C2_delta_norm,'blue',label='natural gradient descent')
plt.plot(C3_delta_norm,'green',label='Gauß-Newton')
plt.legend()
plt.xlabel('iteration')
plt.ylabel(r'$\frac{C(K)-C(K^*)}{C(K^*)}$',usetex=True)
plt.yscale('log')
plt.show()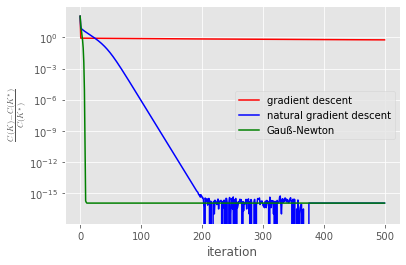

Wie erwartet, konvergiert das Gauß-Newton Verfahren am schnellsten. Danach kommt die natural gradient descent Methode. Die einfache gradient descent-Methode besitzt die geringste Konvergenzrate. Die Lernraten können eventuell noch ein wenig optimiert werden, wahrscheinlich aber nicht allzu viel.

In den Diagrammen scheint die gradient descent-Methode nicht zu konvergieren. Würden wir aber die Anzahl der Iteration deutlich erhöhen, so könnten wir sehen, dass auch diese Methode zum optimalen Regler konvergiert.

Dieser deutliche Unterschied in den Konvergenzraten, zeigt den prinzipiellen Vorteil von natural gradient descent-Methoden gegenüber “vanilla” gradient descent-Methoden.

Zwei natural gradient descent-Methoden im deep reinforcement learning sind mit Trust Region Policy Optimization - TRPO oder Proximal Policy Optimization - PPO gegeben. Die beliebtere PPO-Clip Variante benutzt aber viele “Tricks” und Näherungen, womit es fraglich ist, ob es sich wirklich noch um eine natural gradient descent-Methode handelt. Man kann argumentieren, dass PPO-Clip ähnlich wie Methoden aus den 1990-igern funktioniert.

Fazit

Basierend auf [Fazel et al., 2018] haben wir modellbasierte und modellfrei gradient descent-Methoden besprochen. Die lineare Kontrolltheorie hat sich als hilfreich erwiesen, modellfreie Methoden besser zu verstehen. Der Vorteil ist, dass im linearen Fall modellbasierte Methoden angegeben und vollständig verstanden werden können. Die Idee ist, dass Einsichten welche im linearen Setting gewonnen werden, auch bis zu einem gewissen Grad für auf das deep reinforcement learning übertragbar sind.

In einigen Blogpost haben wir schon gezeigt, wie hilfreich die Kontrolltheorie für das bestärkende Lernen sein kann. Hier nochmals eine Liste der relevanten Artikel:

Bisher haben wir immer zeitdiskrete Systeme behandelt. Da digitale Steuerungen auch so funktionieren, ist dieses Vorgehen sicher gerechtfertigt.

Jedoch werden auch zunehmend zeitkontinuierliche Systeme untersucht, weil physikalische Modelle oft in Form von Differentialgleichung vorliegen. Gerade für modellbasierte Methoden ist daher der zeitkontinuierliche Fall interessant und wird zunehmend erforscht. Erste Papers, welche das bestärkende Lernen im zeitkontinuierlichen Setting untersuchten, wurden jedoch schon in den frühen 1990 Jahren veröffentlicht.

In den nächsten Blogposts wollen wir uns der zeitkontinuierlichen Regelungstechnik zuwenden, aber auch immer wieder auf den zeitdiskreten Fall zurückkommen.